この記事では,2025年11月16日(日)に実施された,「第36回 日本数学オリンピック 予選」の第3問の解答を紹介・解説しています.解答はすべて筆者によるものであり,「公益財団法人 数学オリンピック財団」によるものではありません.
問題については,以下のリンク(公益財団法人 数学オリンピック財団)から閲覧してください(問題の著作権は数学オリンピック財団に帰属します).
第3問は幾何(G)の問題です.三角形の面積の情報と,方べきの定理を用いて線分の長さの比を決定していきます.
問題では図が与えられているが,これを正確に書くと次のようになる.
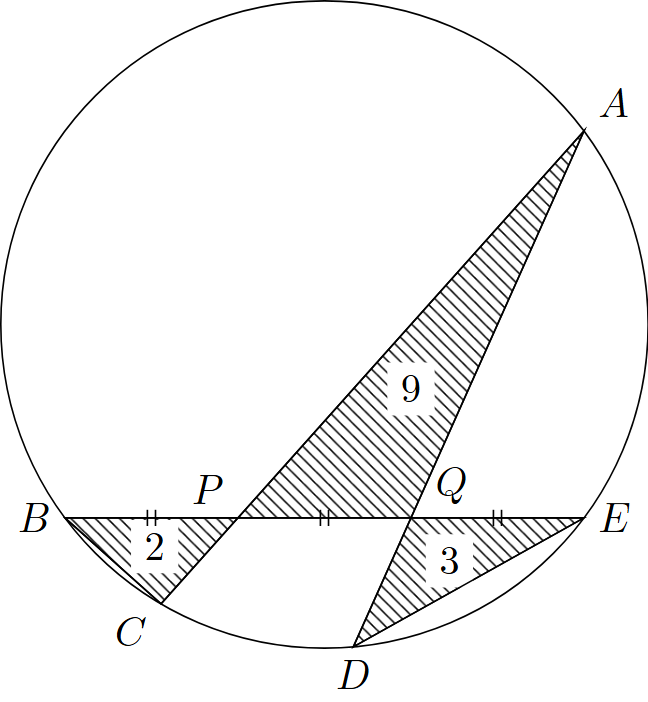
上図を見ると,1つの円とその3つの弦によって構成されていることが分かる.今回求めたい値は2つの弦の長さの比であることに注意しておこう.
問題文で与えられている条件は
- $BP=PQ=QE$
- 三角形$BCP$,三角形$APQ$,三角形$DEQ$の面積はそれぞれ$2,9,3$
の2つである.
この2つの条件に注目すると,三角形$BCP$,三角形$APQ$,三角形$DEQ$は,それぞれ底辺を$BP,PQ,QE$とみると,底辺の長さが等しいことが分かる.よって,三角形$BCP$,三角形$APQ$,三角形$DEQ$の「高さ」の比は面積の比に一致し,$2:9:3$となることが分かる.
もう少し正確に述べると,点$A,C,D$から直線$BE$に下ろした垂線の足をそれぞれ$H_A,H_C,H_D$とすると,三角形$BCP$,三角形$APQ$,三角形$DEQ$の面積はそれぞれ
\[ \frac{1}{2}\cdot BP\cdot CH_C,\quad \frac{1}{2}\cdot PQ\cdot AH_A,\quad \frac{1}{2}\cdot QE\cdot DH_D\]
となる.$BP=PQ=QE$より,三角形$BCP$,三角形$APQ$,三角形$DEQ$の面積の比は,線分$CH_C,AH_A,DH_D$の長さの比に等しく
\[ CH_C:AH_A:DH_D=2:9:3\]
となる.
これで三角形の「高さ」の比を得ることができたが,今注目したいのは弦$AC,AD$である.そこで,この比を使って弦または弦の一部の線分の長さの比を求めてみよう.具体的には,相似な図形を見つけるのである.
実際,三角形$CPH_C$と三角形$APH_A$,三角形$DQH_D$と三角形$AQH_A$は相似である.
三角形$CPH_C$と三角形$APH_A$に注目すると,明らかに
\[ \angle CH_CP=\angle AH_AP=90^{\circ}\]
であり,対頂角は等しいから
\[ \angle CPH_C=\angle APH_A\]
である.よって,二角相等より
\[ \triangle CPH_C\sim \triangle APH_A\]
であるから
\[ CP:AP=CH_C:AH_A=2:9\]
を得る.すなわち,正の実数$k$を用いて
\[ CP=2k,\quad AP=9k\]
と表すことができる.
同様に,三角形$DQH_D$と三角形$AQH_A$に注目すると,明らかに
\[ \angle DH_DQ=\angle AH_AQ=90^{\circ}\]
であり,対頂角は等しいから
\[ \angle DQH_D=\angle AQH_A=90^{\circ}\]
である.よって,二角相等より
\[ \triangle DQH_D\sim \triangle AQH_A\]
であるから
\[ DQ:AQ=DH_D:AH_A=3:9=1:3\]
を得る.すなわち,正の実数$l$を用いて
\[ DQ=l,\quad AQ=3l\]
と表すことができる.
これで,すべての弦の線分の長さについての情報が揃ったことになる.あとは,方べきの定理を用いてこれらの関係を考えよう.
\[ x=BP=PQ=QE\]
とおく.
弦$BE$と弦$AC$に注目すると,方べきの定理より
\[ BP\cdot EP=AP\cdot CP\]
すなわち
\[ 2x^2=18k^2\]
一方,弦$BE$と弦$AD$に注目すると,方べきの定理より
\[ BQ\cdot EQ=AQ\cdot DQ\]
すなわち
\[ 2x^2=3l^2\]
以上より
\[ 18k^2=3l^2\]
すなわち
\[ 6k^2=l^2\]
求める値は
\[ \frac{AC}{AD}=\frac{11k}{4l}=\frac{11}{4}\cdot \frac{k}{l}\]
である.ここで
\[ \left( \frac{k}{l}\right) ^2=\frac{k^2}{l^2}=\frac{1}{6}\]
より
\[ \frac{k}{l}=\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}\]
であるから
\[ \frac{AC}{AD}=\frac{11}{4}\cdot \frac{\sqrt{6}}{6}=\frac{11\sqrt{6}}{24}\]
ここまでの議論を簡潔に整理すると,次のようになる.
点$A,C,D$から直線$BE$に下ろした垂線の足をそれぞれ$H_A,H_C,H_D$とし
\[ x=BP=PQ=QE\]
とする.
\[ \triangle CPH_C\sim \triangle APH_A\\ \triangle DQH_D\sim \triangle AQH_A\]
より
\[ CP:AP=CH_C:AH_A\\ DQ:AQ=DH_D:AH_A\]
また
\[ CH_C:AH_A:DH_D=\triangle BCP:\triangle APQ:\triangle DEQ=2:9:3\]
であるから
\[ CP:AP=2:9\\ DQ:AQ=1:3\]
よって,ある正の実数$k,l$が存在して
\[ CP=2k,\quad AP=9k\\ DQ=l,\quad AQ=3l\]
となる.
方べきの定理より
\[ BP\cdot EP=AP\cdot CP\\ BQ\cdot EQ=AQ\cdot DQ\]
であるから
\[ 2x^2=18k^2\\ 2x^2=3l^2\]
すなわち
\[ \frac{k^2}{l^2}=\frac{1}{6}\]
を得る.よって
\[ \frac{k}{l}=\frac{1}{\sqrt{6}}=\frac{\sqrt{6}}{6}\]
であるから
\[ \frac{AC}{AD}=\frac{11k}{4l}=\frac{11}{4}\cdot \frac{\sqrt{6}}{6}={\color{red}\frac{11\sqrt{6}}{24}}\]
参考文献
- 公益財団法人 日本数学オリンピック財団, https://www.imojp.org(最終閲覧日は当記事の最終更新日です).

