MathAbyssによる数学問題集,好評発売中.
2026年のための数学問題集『Problems and Puzzles 2026』
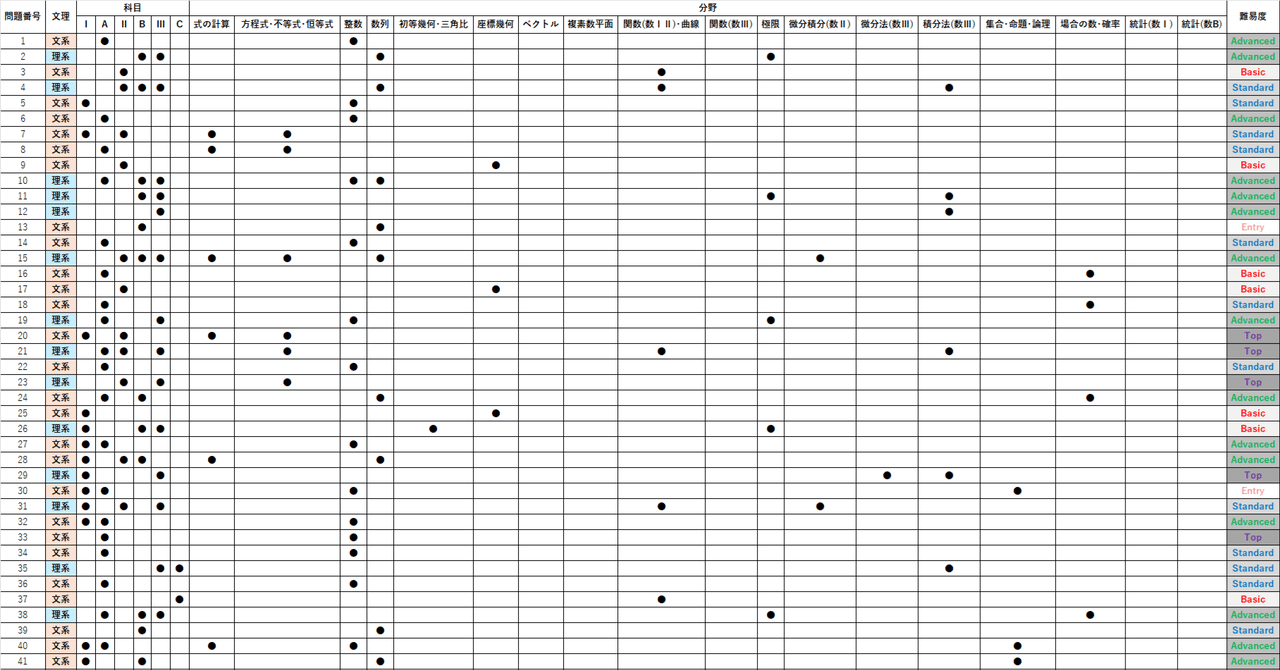
圧倒的な難易度の問題に立ち向かえ.『受験数学総合演習50』
MathAbyssへようこそ!
MathAbyssでは,「難解な数学を,簡潔に・厳密に・丁寧に」解説した記事を公開しています.
最新情報は以下のページをご覧ください.
Let’s Share!
Follow us!
新着記事
人気記事
記事一覧
分野別に記事を整理しています.順次,記事を追加予定です.
近日公開予定の記事のリンクは閲覧できません.ご了承ください.
高校数学
高校数学を,「本質的な理解」と「問題を解く」ことに焦点を当て,シンプルかつ徹底的に解説.
場合の数
確率
図形の性質
式と証明
複素数と方程式
図形と方程式
三角関数
指数関数・対数関数
微分法
積分法
数列
統計的な推測
関数
極限
微分法
微分法の応用
積分法
積分法の応用
平面ベクトル
- ベクトル
- ベクトルの和とスカラー倍
- 1次独立と1次従属
- ベクトルの成分表示
- ベクトルの内積
- ベクトルの内積と不等式
- 位置ベクトルと図形
- 交点の位置ベクトル
- 三角形の五心の位置ベクトル
- ベクトルの終点の存在範囲
- ベクトル方程式
- 斜交座標
空間ベクトル
複素数平面
式と曲線
数学の全体像シリーズ
大学数学の内容を分野別に総整理.全体を俯瞰し,個別の内容の理解を深めよう.
問題解説
「新作問題Problems」では,MathAbyssが作問・改題した,一捻りのある問題を紹介.
中学入試,高校入試,大学入試,院試,競技数学の良問を,解くときの思考回路を完全再現して徹底的に解説.
数学基礎論
集合論,実数論,位相空間論,圏論を徹底解説.
命題論理
集合
写像
- 写像
- 像と逆像
- 全射と単射
- 合成写像
- 定義域と値域・始集合と終集合
- 写像の集合
- 元の族
- 集合族
- 集合族の直積
- 選択公理
- 多変数写像
同値関係
- 二項関係
- 同値関係
- 同値類・商集合
- 標準全射
濃度
- 対等関係
- ベルンシュタインの定理
- 濃度
- 濃度の大小
- 可算集合
- 可算集合の性質
- 非可算集合
- カントールの定理
- 濃度の和と積
- 濃度の累乗
- 可算濃度と連続体濃度の演算
順序
- 順序関係
- 順序集合
- 最大元と最小元・極大元と極小元・上限と下限
- 順序同型写像
- 双対順序
整列集合
- 整列集合
- 超限帰納法
- 整列集合の順序同型
- 整列集合の比較定理
- ツォルンの補題
- ツォルンの補題と同値な命題
- 整列可能定理
- ツォルンの補題と濃度
- 基底の延長定理・基底の存在定理
順序数
- 順序数
- 順序数の大小
- 順序数の演算
- 順序数と濃度
その他
- 連続体仮説
自然数
- 自然数の定義
- 自然数の一意性
- 自然数の加法
- 自然数の乗法
- 自然数の大小
- 自然数の簡約法則
- 自然数の整列性
- 自然数の自然数乗
整数
- 整数の定義
- 整数の一意性
- 整数の加法・減法
- 整数の乗法
- 整数の大小
- 整数の簡約法則
- 整数の絶対値
- 倍数と約数
- 素数・素因数分解
有理数
- 有理数の定義
- 有理数の一意性
- 有理数の加法・減法
- 有理数の乗法・除法
- 有理数の大小
- 有理数の簡約法則
- 有理数の稠密性
- 有理数の絶対値
- 有理数の整数乗
実数
- デデキントの切断による実数の定義
- 有理数の完備化による実数の定義
- 実数の大小
- 実数の加法・減法
- 実数の乗法・除法
- 実数の絶対値
- 実数列の極限
- 実数の完備性
- 実数の連続性
- 実区間
- 最大値と最小値・上限と下限
- 実数の一意性
- 実関数の連続性
ユークリッド空間
- ユークリッド空間
- ユークリッド空間の開集合・閉集合
- ユークリッド空間の点列
- 多変数写像の連続性
- 行列の集合
複素数
- 複素数の定義
- 複素数の四則演算
- 複素数の絶対値
- 複素平面
- 代数学の基本定理
ユークリッド空間
距離空間
位相空間
位相空間の性質
- 連結空間
- 局所連結空間
- コンパクト空間
- チコノフの定理
- ハウスドルフ空間
- 分離公理
- 局所コンパクト空間
- パラコンパクト空間
- コンパクト化
解析学
微分積分学,ベクトル解析学,複素関数論,微分方程式論,フーリエ解析学,確率論を徹底解説.
実数
- 実数の四則演算
- 実数の大小関係
- 最大値と最小値・上界と下界・上限と下限
- 絶対値・三角不等式
- 実数の連続性
- 上限と下限の性質
- 自然数・整数・有理数
- 数列と極限
- 数列の極限と四則演算
- 数列の極限と不等式
- 数列の単調性
- 有界単調数列の収束定理
- アルキメデスの原理
- 区間
- 区間縮小法
- 部分列
- ボルツァーノ・ワイエルシュトラスの定理
- コーシー列
- 連続の公理
- 有理数の稠密性
ユークリッド空間
- 数空間
- ベクトル空間
- ユークリッド空間
- ノルムと距離
- 点列と極限
- 2次元ユークリッド空間と複素数
- 複素数の性質
級数
- 拡大実数
- 拡大実数の点列の極限
- 上極限と下極限
- 級数の収束と発散
- 絶対収束と条件収束
- 比較判定法
- コーシーの判定法
- ダランベールの判定法
- 正項級数の収束性
関数
- 閉包
- 関数と極限
- 点列の極限と関数の極限
- 関数の極限の性質
- 関数の連続性
- 関数の極限と四則演算
- 合成関数
- 関数の収束とコーシーの収束条件
- 関数列と各点収束
- ワイエルシュトラスのM判定法
- 点列コンパクト
- 関数の最大値と最小値
- 被覆
- ハイネ・ボレルの被覆定理
- 中間値の定理
- 開集合の連結性
- 開集合と閉集合の性質
1変数関数の微分法
- 実関数の微分
- 実関数の微分の性質
- 片側極限・片側連続・片側微分
- 関数の極値
- ロルの定理・平均値の定理
- 関数の単調性
- ロピタルの定理
- 高次導関数
- 関数の凹凸
- 実変数のテイラーの定理
- テイラー展開
- 凸関数
- ニュートンの逐次近似法
- 方向微分
- 偏微分
- 偏微分の交換
- 連続微分可能性
- ランダウの記号
- 関数の同値
- 漸近展開
多変数関数の微分法
- 多変数実数値関数の微分
- 接超平面
- 多変数実数値関数と微分可能性
- 勾配
- 多変数ベクトル値関数の微分
- 多変数ベクトル値関数の微分可能性と連続性
- 多変数ベクトル値関数の微分と和・定数倍
- 連鎖律
- ヤコビアン
- 多変数ベクトル値関数の積の微分法
- 合成関数の2階偏導関数
- 有限増分の定理
- 逆関数定理
- 多変数のテイラーの定理
- 多変数関数の極値
- 2次形式と関数の最大値・最小値
- 2次形式の性質と同値な命題
- 2次形式と関数の極値
- 微分形式
- 外微分
- 微分形式の引き戻し
代数学
線形代数学,群論・環論・体論,整数論,表現論を徹底解説
幾何学
初等幾何学,位相空間論,非ユークリッド幾何学,代数幾何学,微分幾何学を徹底解説.
離散数学
グラフ理論,組合せ論を徹底解説.
数理科学
統計学,数値解析学,計算機科学,数理物理学を徹底解説.
数学史
数学史を徹底解説.
$\TeX$
理系学生は必須の$\TeX$の使い方を徹底解説.
Python
Pythonの使い方を徹底解説.
その他
- 大学数学の学び方を徹底解説
- 過去最大の素数が発見!
- 2025にまつわる超良問!
- 【徹底分析】令和7年度 大学入学共通テスト 数学Ⅰ,数学A
- 【徹底分析】令和7年度 大学入学共通テスト 数学Ⅱ,数学B,数学C
- 【PDF有】2025年度 国立10大学 数学 入試問題
- 【徹底分析】令和8年度 大学入学共通テスト 数学Ⅰ,数学A
- 【徹底分析】令和8年度 大学入学共通テスト 数学Ⅱ,数学B,数学C
- 【PDF有】2026年度 国立10大学 数学 入試問題
当サイトの記事では,様々な書籍,学術系PDFファイル,Webサイトを参考文献としています.基本的な参考文献のリストは以下のページに掲載しております.