この記事では,2025年11月16日(日)に実施された,「第36回 日本数学オリンピック 予選」の第7問の解答を紹介・解説しています.解答はすべて筆者によるものであり,「公益財団法人 数学オリンピック財団」によるものではありません.
問題については,以下のリンク(公益財団法人 数学オリンピック財団)から閲覧してください(問題の著作権は数学オリンピック財団に帰属します).
第7問は組合せ論(C)の問題です.直接数えるのは難しそうなので,簡単に数え上げられるものに対応させる必要があります.2つの気づきが必要です.
いきなり$2026$人について考えるのは難しい.そこで,人数を減らして考えたい.例として,$10$人の生徒を考え,行動を終えたときの$1$人以上の生徒が座っているベンチの数を$7$台として考えてみよう.
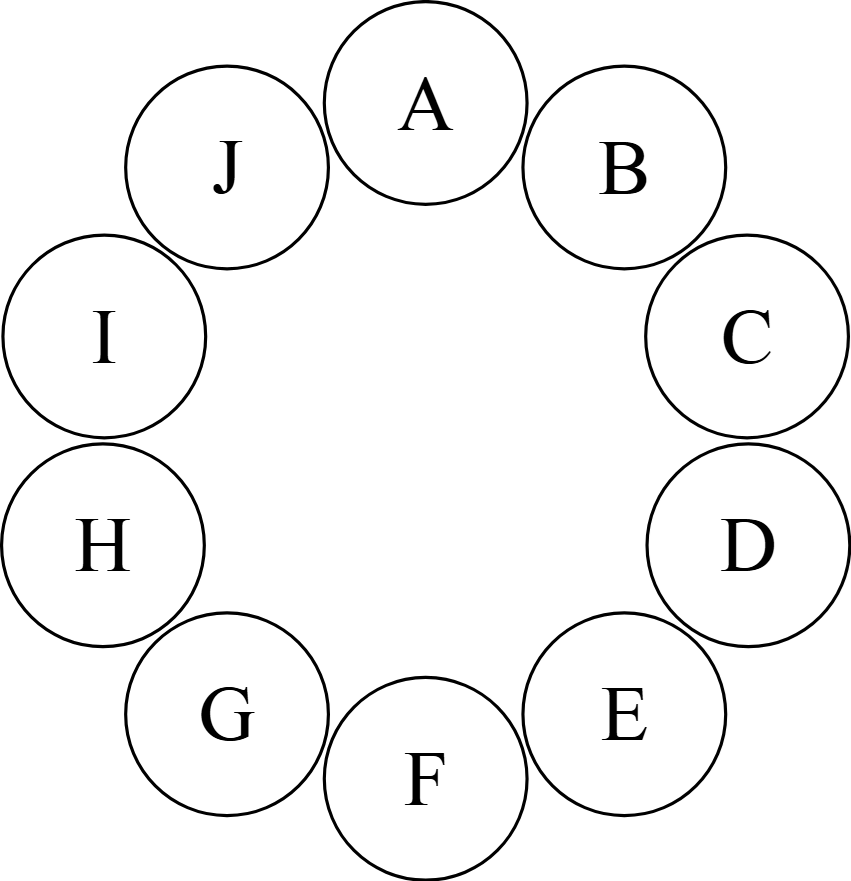
まず,上図のように10台のベンチを配置し,そこに座っている生徒を$\rm A,B,\dots ,J$とする.
例えば,先生が$\rm A,C,D,G$の$4$人の生徒を選んだとする.
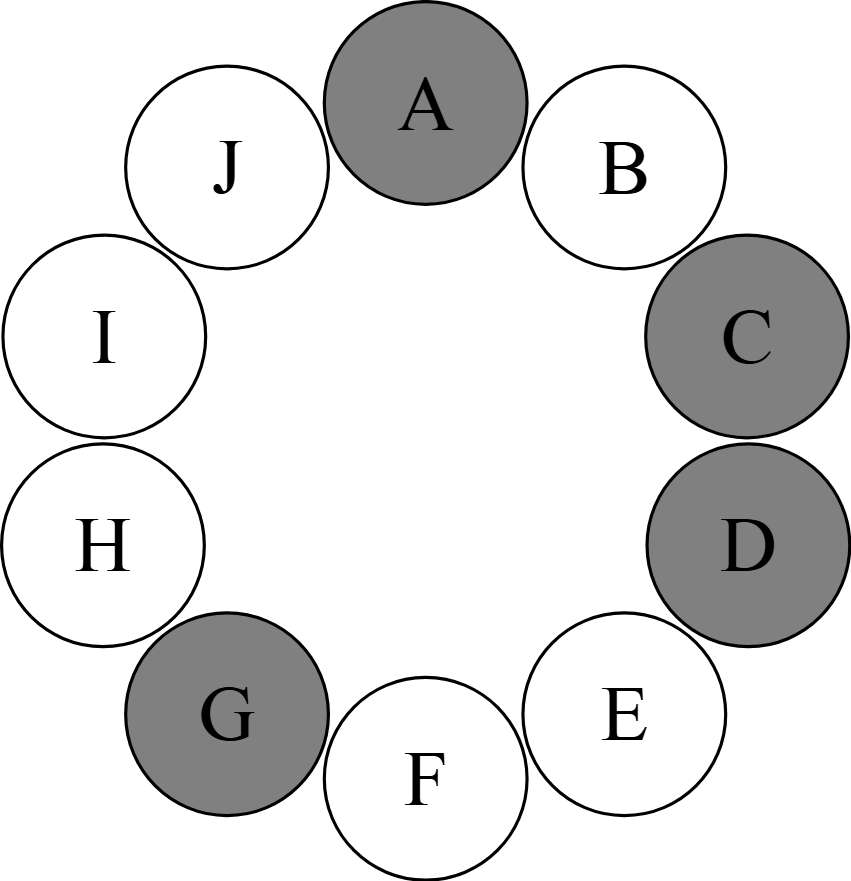
このとき,問題文に書かれているように行動すると,次のようになる.
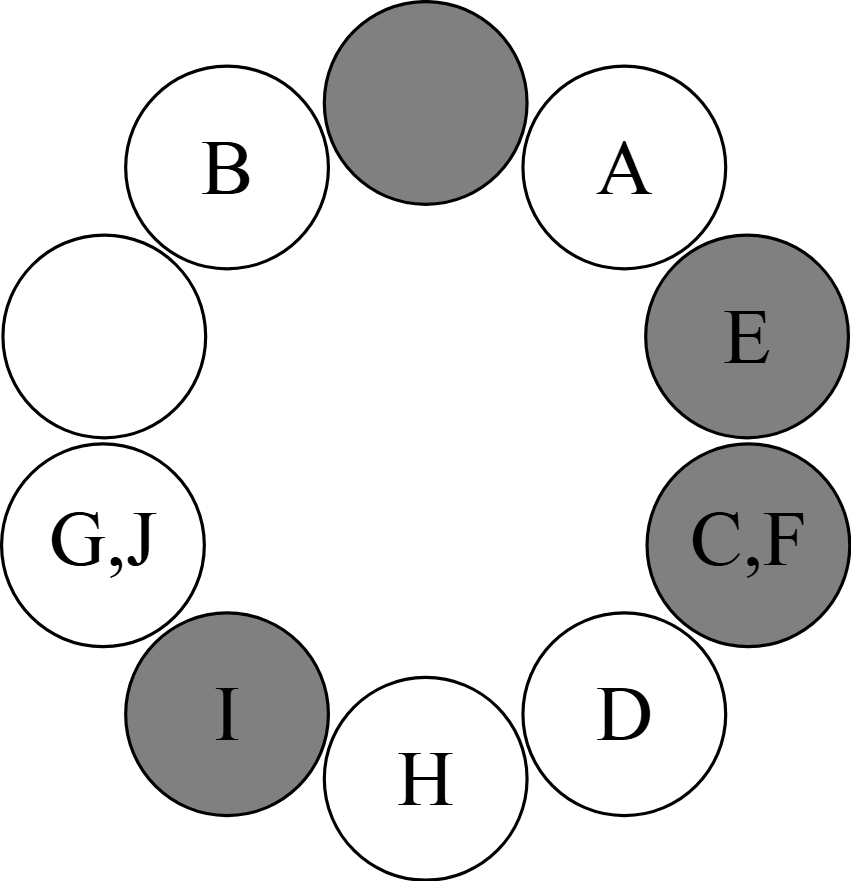
すると,$1$人以上の生徒が座っているベンチは$8$台であり,特に$2$台のベンチに$2$人の生徒が座っている.
この例のように,行動を終えたとき,各ベンチに座っている生徒の人数は$0,1,2$のいずれかであり,$0$人の生徒が座っているベンチの台数と$2$人の生徒が座っているベンチの台数は等しい.
よって,この台数を数えることが目標となる.
また,行動に注目すると,選ばれた生徒は時計回りに$1$つ隣に進み,選ばれなかった生徒は反時計回りに$2$つ進んでいる.これは,選ばれた生徒が時計回りに$3$つ進み,選ばれなかった生徒は動かないように行動しても同じ結果が得られる.
ただし,ここでいう「同じ結果」とは,$1$人以上の生徒が座っているベンチの台数が変わらないということを指している.
したがって,ここからは
「選ばれた生徒が時計回りに$3$つ進み,選ばれなかった生徒は動かない」
という行動に置き換えて考えることにする(この立場では,選ばれた生徒に注目すればよいため,問題を考えやすい).
さて,ベンチが「行動を終えた後に生徒が座っていない」状態になるための必要十分条件は,最初に座っていた生徒が先生に選ばれ,かつ,$3$つ左のベンチに最初に座っていた生徒が先生に選ばれないことである.
先ほどの例では,最初に$\rm A$が座っていたベンチは,行動を終えた後に生徒が座っていないことが分かる.実際,最初に座っていた生徒$\rm A$は先生に選ばれ,かつ,$3$つ左のベンチに最初に座っていた生徒$\rm H$は先生に選ばれていない.
また,ベンチが「行動を終えた後に$2$人の生徒が座っている」状態になるための必要十分条件は,最初に座っていた生徒が先生に選ばれず,かつ,$3$つ左のベンチに最初に座っていた生徒が先生に選ばれることである.
先ほどの例では,最初に$\rm F$が座っていたベンチは,行動を終えた後に$2$人の生徒が座っていることが分かる.実際,最初に座っていた生徒$\rm F$は先生に選ばれておらず,かつ,$3$つ左のベンチに最初に座っていた生徒$\rm C$は先生に選ばれている.
つまり,ベンチが「行動を終えた後にちょうど$1$人の生徒が座っている」状態であるかどうかは,そのベンチに最初に座っていた生徒と,そのベンチの$3$つ左のベンチに最初に座っていた生徒にのみ注目すれば良いことが分かる.
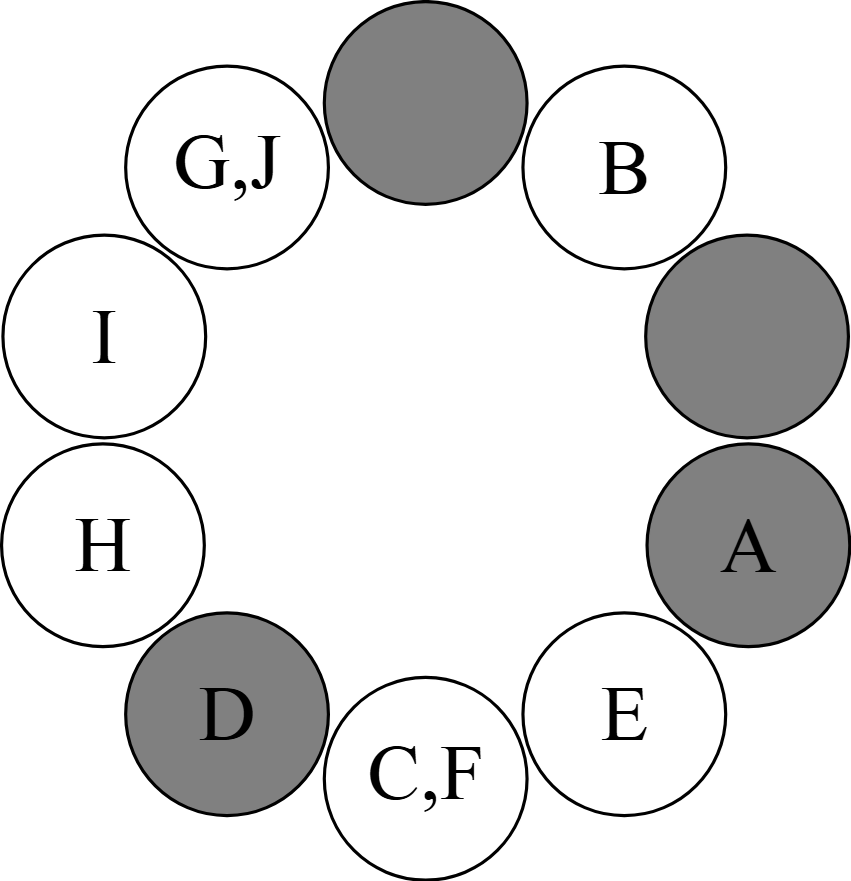
そこで,ベンチに次のように番号を振ってみよう.
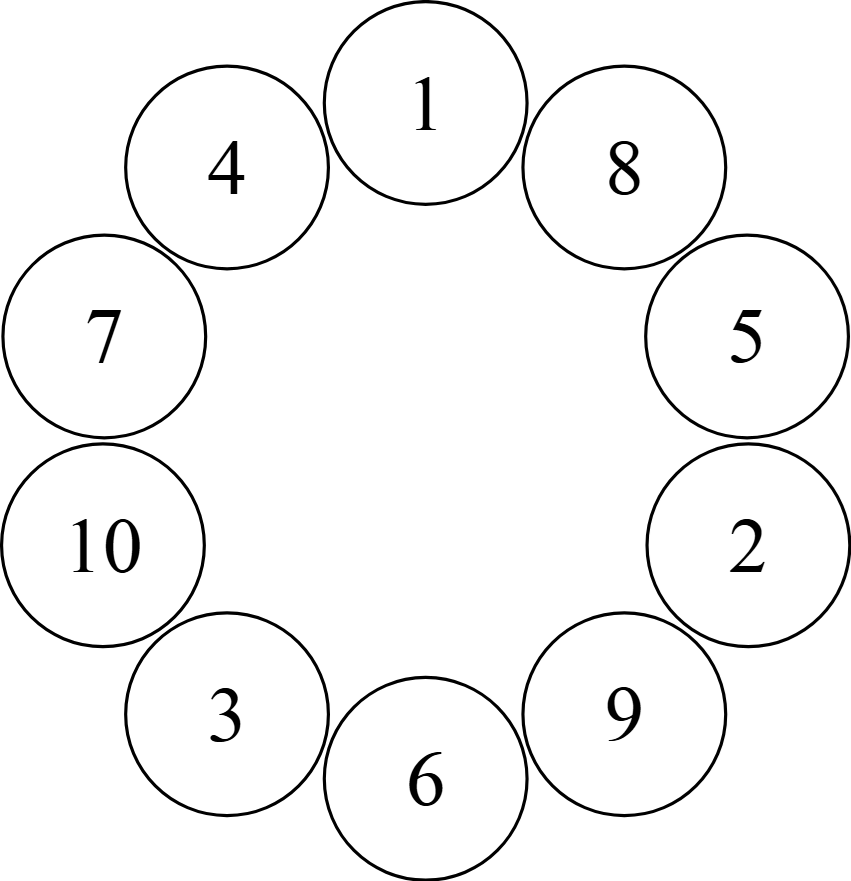
上図では,まず,最初に$\rm A$が座っていたベンチを$1$とし,その後,時計回りに$2$つのベンチを飛ばして番号を振っている.
すると,行動を終えた後に,例えば$2$のベンチに何人の生徒が座っているのかを知りたければ,$1$と$2$のベンチに注目すれば良いことが分かる.
要するに,行動を終えた後に$i$のベンチに何人の生徒が座っているのかを知りたければ,$i$と$i-1$のベンチに注目すれば良いということである(ただし,$i$は$1$以上$10$以下の整数であり,$0$のベンチは$10$のベンチとみなす).
そして,ここからがこの問題をエレガントに解く要となる発想なのだが,以上の議論から,生徒の行動は次のように考えることができる.
「選ばれた生徒が今座っているベンチの番号に$1$を足した番号のベンチに座り,選ばれなかった生徒は動かない」
(ただし,$11$のベンチは,それぞれ$1$のベンチとみなす)
このように考えると,「何個隣のベンチに移動するか」という情報が抜けている.つまり,「何個隣のベンチに移動するか」は関係ないということである.
それならば,最も単純な「時計回りに$1$個隣のベンチに移動する」場合について考えよう.具体的には,ベンチの場所を次のように入れ替える.
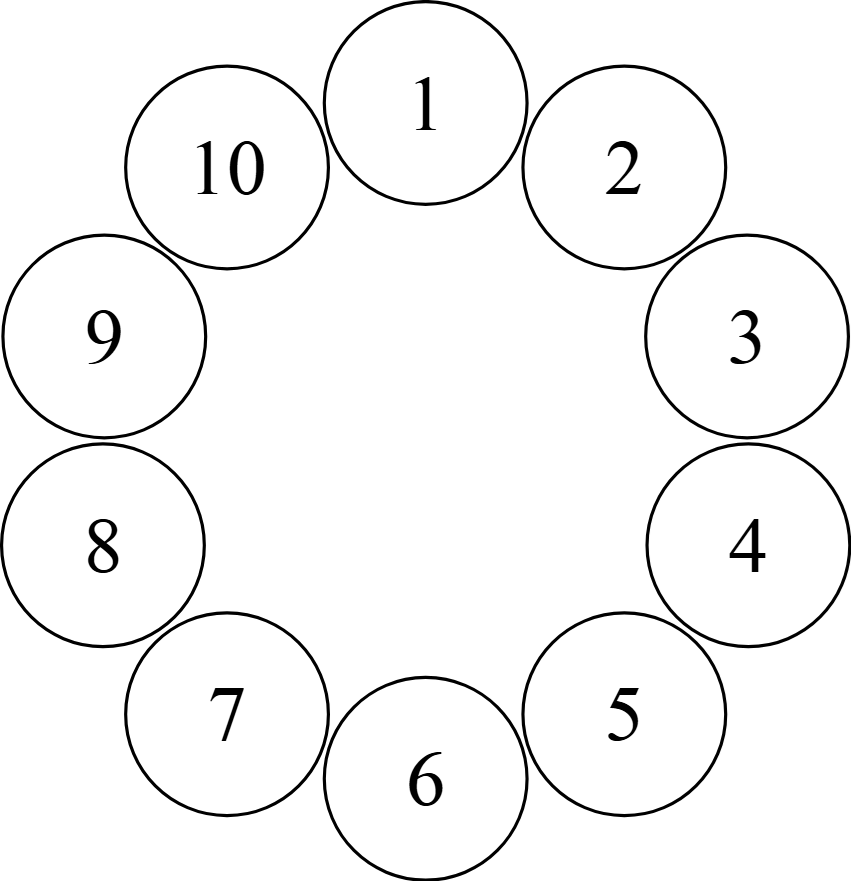
すると,生徒の行動は
「選ばれた生徒が時計回りに$1$つ進み,選ばれなかった生徒は動かない」
という非常にシンプルなものになった.以下,この行動について考える.
ここまで考えてきた問題は,最初に$10$台のベンチと$10$人の生徒がいる状況であり,行動を終えたとき,$1$人以上の生徒が座っているベンチの台数がちょうど$7$台,すなわち$0$人の生徒が座っているベンチが$3$台であるような生徒の選び方が何通りあるか,というものであった.
先程と同様に,ベンチが「行動を終えた後に生徒が座っていない」状態になるための必要十分条件を考えると,最初に座っていた生徒が先生に選ばれ,かつ,$1$つ左のベンチに最初に座っていた生徒が先生に選ばれないことである.
では,このような生徒の選び方はどのように数えればよいだろうか.
これまた先程と同様に,選ばれた生徒が最初に座っているベンチに色を付け,行動する前と行動した後の生徒の座っている位置の変化に注目すると,下図のようになる.

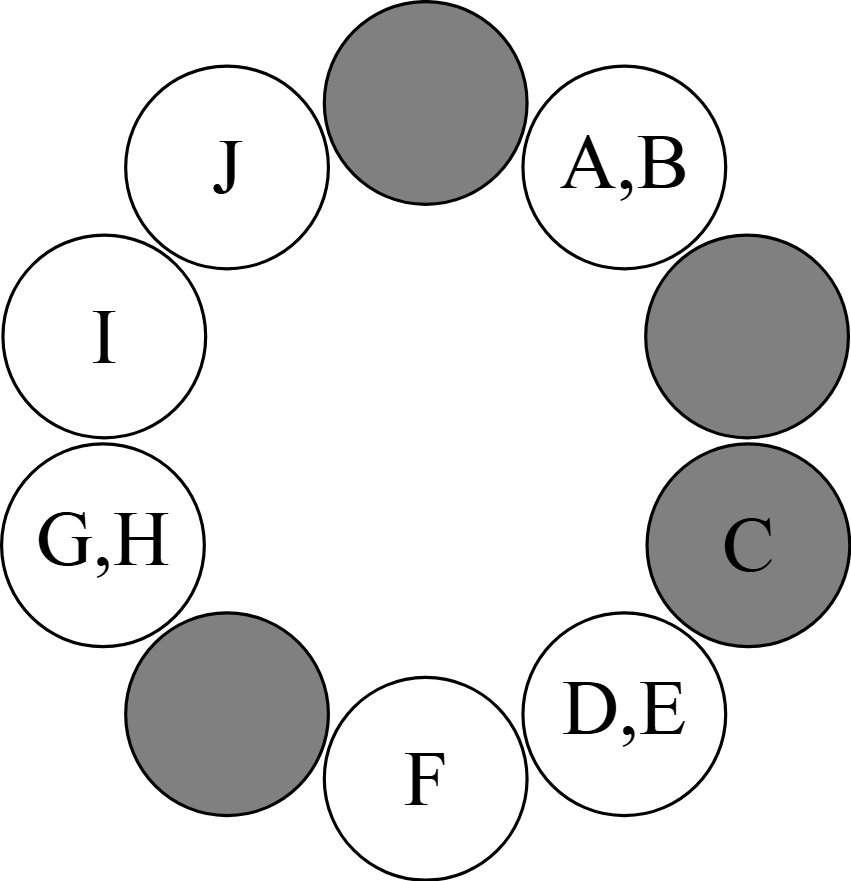
すなわち,「行動を終えた後に生徒が座っていない」ベンチの数は,「色がついていないベンチと色がついているベンチがこの順で時計回りに並んでいる箇所」の数に等しいことが分かる.
例えば,上図においては
\[ \rm A,B,C,D,E,F,G,H,I,J\]
の$10$人の生徒を
\[ \rm A\mid B\mid C,D\mid E,F\mid G\mid H,I,J\mid \]
のように$6$つにグループ分けし,左から順に,「先生が選ぶ生徒のグループ」,「先生が選ばない生徒のグループ」,と交互に決めていくと,「色がついていないベンチと色がついているベンチがこの順で時計回りに並んでいる箇所」が$3$つできている.
つまり,円形に並んだ$10$台のベンチの間に$6$つの仕切りを入れ,これによって分けられた$6$つのグループについて,時計回りに,「先生が選ぶ生徒のグループ」,「先生が選ばない生徒のグループ」,と交互に決めていくと,「行動を終えた後に生徒が座っていない」ベンチの数が$3$つになるということである.
円形に並んだ$10$台のベンチの間に$6$つの仕切りを入れる方法の総数は,ベンチとベンチの間$10$箇所から$6$箇所を選ぶ方法の総数${}_{10}\mathrm{C}_6$通りであり,これによって分けられた$6$つのグループについて,「先生が選ぶ生徒のグループ」と「先生が選ばない生徒のグループ」の振り分け方が$2$通りある.
よって,最初に$10$台のベンチと$10$人の生徒がいる状況であり,行動を終えたとき,$1$人以上の生徒が座っているベンチの台数がちょうど$7$台,すなわち$0$人の生徒が座っているベンチが$3$台であるような生徒の選び方は
\[ {}_{10}\mathrm{C}_6\times 2=420(通り)\]
である.
それでは,本問についても同様に考えてみよう.
「行動を終えた後に生徒が座っていない」ベンチの数が$26$台であればよいから,$2026$台のベンチを$2\times 26=52$個のグループに分ければよい.よって,先程と同様に考えると
\[ 2\times {}_{2026}\mathrm{C}_{52}(通り)\]
である.
ここまでの議論を簡潔に整理すると,次のようになる.
$i$を$1$以上$2026$以下の整数とする.
まず,生徒の行動を
- 先生に選ばれた生徒は,自分の座っているベンチの$3$台右にあるベンチへ移動して座る.
- 先生に選ばれなかった生徒は,自分の座っているベンチに座り続ける.
としても,求める方法の総数は変わらない.
ここで,$1$台のベンチ$B_1$を任意に固定し,$2026$台のベンチを,$B_1$から時計回りに$3$台おきに$B_2,B_3,\dots ,B_{2026}$とする.
また,各ベンチ$B_i$に最初に座っている生徒を$A_i$とする.
このとき,生徒の行動は次のように言い換えることができる.
- 先生に選ばれた生徒$A_i$は,自分の座っているベンチ$B_i$からベンチ$B_{i+1}$へ移動して座る.
ただし,$B_{2027}=B_1$とする. - 先生に選ばれなかった生徒は,自分の座っているベンチに座り続ける.
よって,ベンチの位置を時計回りに$B_1,B_2,\dots ,B_{2026}$の順に円形に並べ直し,最初に各生徒$A_i$をベンチ$B_i$に座らせても,求める方法の総数は変わらない.
ゆえに,生徒の行動を
- 先生に選ばれた生徒は,自分の座っているベンチの$1$台右にあるベンチへ移動して座る.
- 先生に選ばれなかった生徒は,自分の座っているベンチに座り続ける.
としても,求める方法の総数は変わらない.
さて,生徒が行動を終えた後,ベンチ$B_i$に座っている生徒の人数が$0$であるための必要十分条件は,次の2つの条件をみたすことである.
- 先生が生徒$A_i$を選ぶ.
- 先生が生徒$A_{i-1}$を選ばない.
ただし,$A_0=A_{2026}$とする.
よって,求める方法の総数は,最初に互いに隣のベンチに座っている$2$人の生徒の組であって,左側の生徒が先生に選ばれず,右側の生徒が先生に選ばれるようなものが$26$組あるような,生徒の選び方の総数に等しい.
円形に並ぶ$2026$台のベンチについて,ベンチとベンチの間$2026$箇所から$52$箇所を選び,仕切りを入れると,ベンチは$52$のグループに分けられる.これらのグループを,ベンチ$B_1$を含むグループから,時計回りに$G_1,G_2,\dots ,G_{52}$とする.
$G_1,G_3,\dots ,G_{51}$の$26$のグループのいずれかに属する生徒と,$G_2,G_4,\dots ,G_{52}$の$26$のグループのいずれかに属する生徒のうち,先生が一方の生徒を選び,一方の生徒を選ばないとき,生徒が行動を終えた後に座っている生徒の人数が$0$であるようなベンチの数は$26$となる.
したがって,求める方法の総数は
\[ {\color{red}2\times {}_{2026}\mathrm{C}_{52}}(通り)\]
参考文献
- 公益財団法人 日本数学オリンピック財団, https://www.imojp.org(最終閲覧日は当記事の最終更新日です).

