第36回(2026年) JMO 予選第6問

この記事では，2025年11月16日(日)に実施された，｢第36回 日本数学オリンピック 予選｣の第6問の解答を紹介･解説しています．解答はすべて筆者によるものであり，｢公益財団法人 数学オリンピック財団｣によるものではありません．

問題については，以下のリンク(公益財団法人 数学オリンピック財団)から閲覧してください(問題の著作権は数学オリンピック財団に帰属します)．

日本数学オリンピック概要

JMO, 日本数学オリンピック

www.imojp.org

第6問は幾何(G)の問題です．まずは図を描き，どのような補助線を引くべきかを考えてみよう．特に，平行四辺形が絡む構図は相似な三角形をつくることが有効である．

問題の状況を把握するために，図を描いてみると次のようになる．

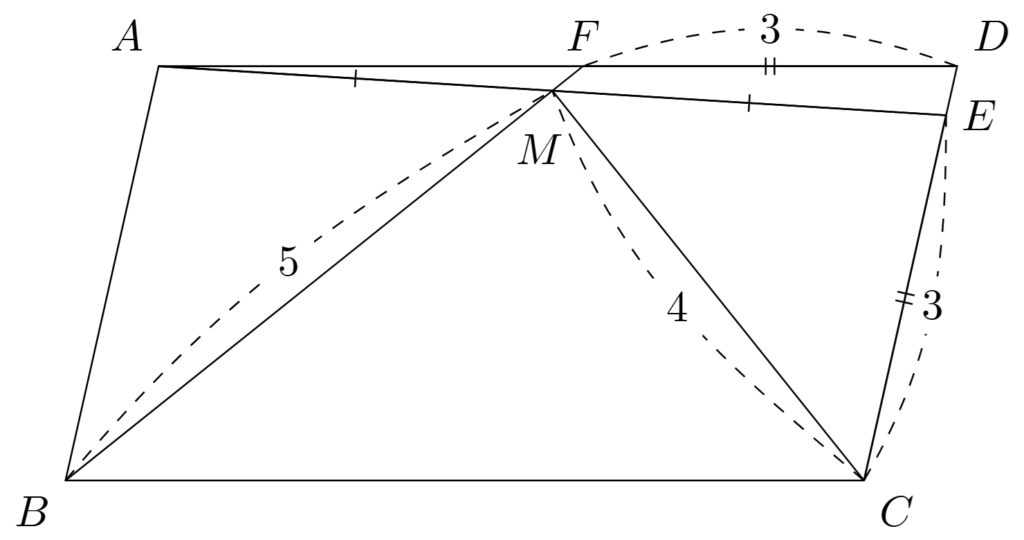
この問題を解くに当たって意識しなければならないのは，平行四辺形には相似な図形がたくさん現れるということである．これは，平行四辺形が｢向かい合う辺が平行である｣ことに由来する．そのため，平行四辺形と，その周辺に線分が与えられたとき，平行四辺形の辺や与えられた線分を延長することによって得られる交点を考えることによって，相似な三角形を作ることができる場合が多い．

一般論はここまでにしておいて，本問に取り組んでいこう．まず，今回は$4$つの線分について，その具体的な長さが与えられているが，一度それは忘れて，$AM=EM$と$CE=DF$をどのように利用するべきかを考えよう．

$CE$と$DF$は少し扱いにくい位置にあるため，まず$AM$と$EM$について考えてみる．先ほどの一般論と合わせて考えると，最も自然な発想は，直線$BF$と直線$CD$の交点$G$をとり，三角形$ABM$と三角形$EGM$に注目することである．

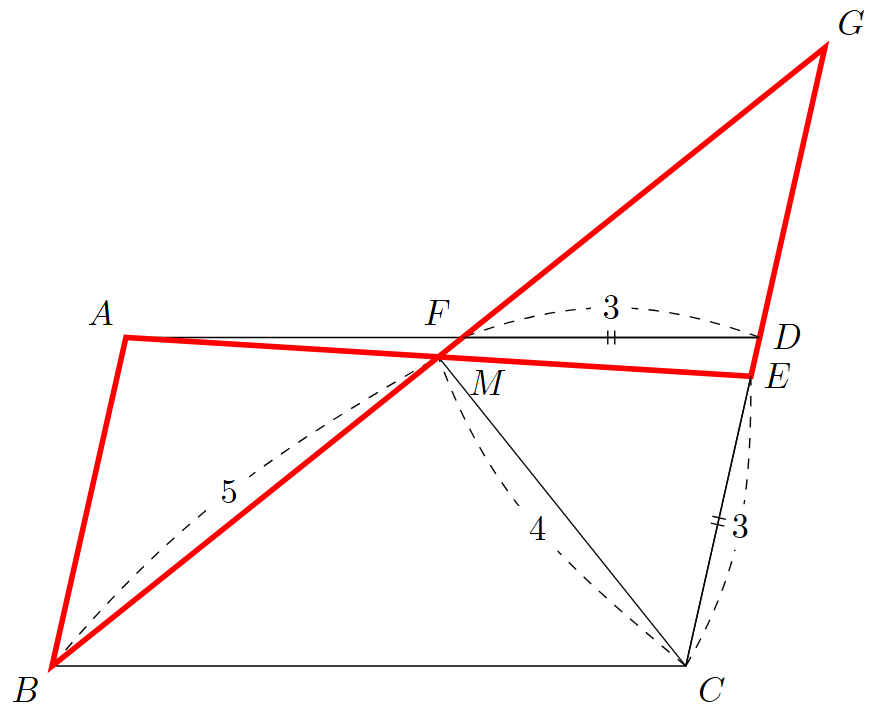
対頂角の大きさは等しいから
\[ \angle AMB=\angle EMG\]
また，$AB/\!/CD$より，平行線の錯角の大きさは等しいから
\[ \angle MAB=\angle MEG\]
$AM=EM$であるから，二角夾辺相等より
\[ \triangle ABM\equiv \triangle EGM\]
であることが分かる．ここから直ちに得られることとして
\[ AB=EG=CD,\quad BM=GM=5\]
がある．

ここで，$x=AB$とおくと
\[ CG=CE+EG=x+3\]
であるから，$CD=x$より，$DG=3$であることが分かる．すなわち，三角形$DFG$は$DF=DG=3$の二等辺三角形である．

$AD/\!/BC$より，平行線の同位角の大きさは等しいから
\[ \angle GFD=\angle GBC\\ \angle GDF=\angle GCB\]
よって，二角相等より
\[ \triangle GFD\sim \triangle GBC\]
特に，三角形$CBG$は$CB=CG$の二等辺三角形である．

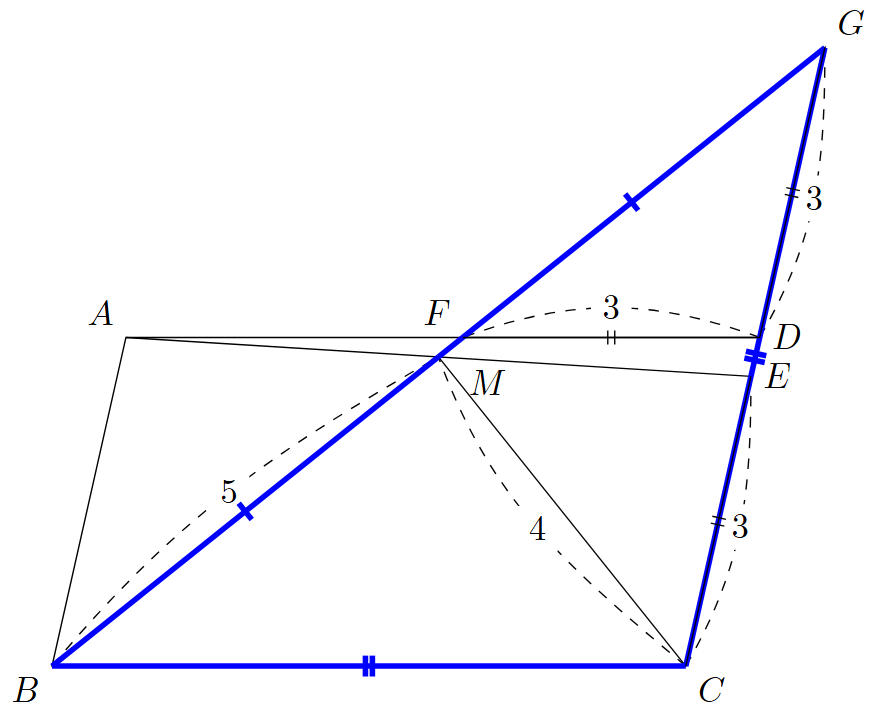
$M$が，二等辺三角形$CBG$の頂角と向かい合う辺$BG$の中点であることに注意すると，$\angle CMB=90^{\circ}$であるから，三平方の定理より
\[ (x+3)^2=5^2+4^2\]
よって
\[ x=\sqrt{41}-3\]
であることが分かった．

ここまでの議論を簡潔に整理すると，次のようになる．

参考文献

• 公益財団法人 日本数学オリンピック財団, https://www.imojp.org(最終閲覧日は当記事の最終更新日です).