複素平面

複素数を視覚的･直感的に理解するために欠かせない複素平面を導入する．

複素平面

写像$f:\mathbb{R}^2\to \mathbb{C}$を
\[ f(a,b)=a+bi\quad (a,b\in \mathbb{R})\]
により定めると，$f$は全単射である．よって，この逆写像$f^{-1}$によって，複素数を平面$\mathbb{R}^2$の点として，1対1に対応付けすることができる．

平面上に，横軸として複素数の実部を表す実軸(real axis)をとり，それに直交する縦軸として，複素数の虚部を表す虚軸(imaginary axis)をとると，任意の複素数を平面上の1点に対応付けることができる．

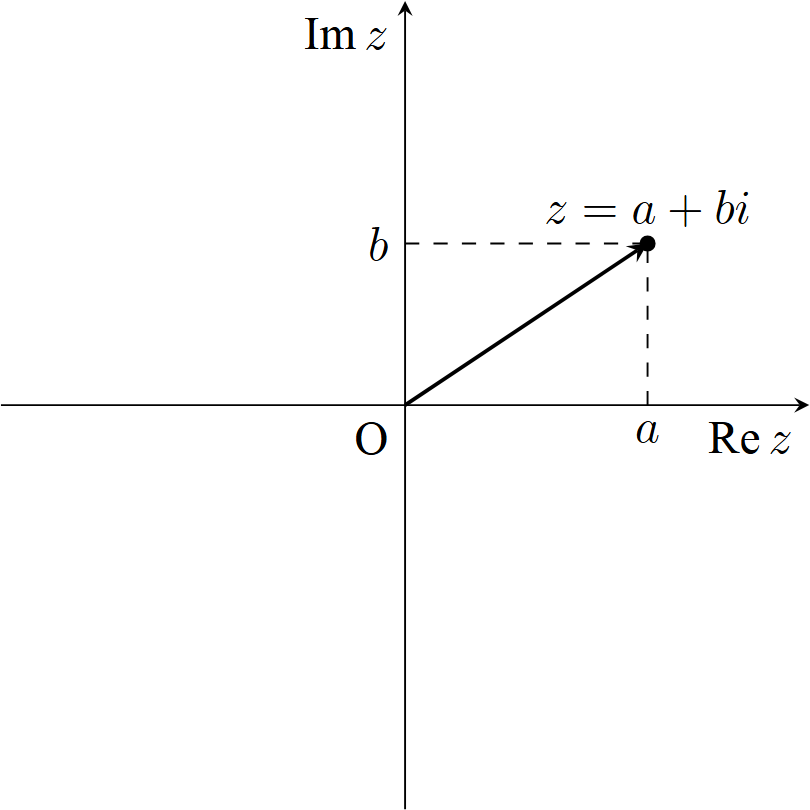
この平面を複素平面(または複素数平面)(complex plane)(またはガウス平面(Gaussian plane)，$z$-平面($z$-plane))という．

ところで，複素平面上の1点$z$は，原点からの距離$r$と，原点と$z$を結ぶ線分($z$の動径)と実軸の正の部分がなす角$\theta$(弧度法を用いる)を用いて表すことができる．
このとき，$r=|z|$であり，$\theta$は$z$の偏角(argument)といい，$\arg z$で表す¹．

すなわち，任意の複素数は絶対値と偏角を用いて表すことができ，以下の図

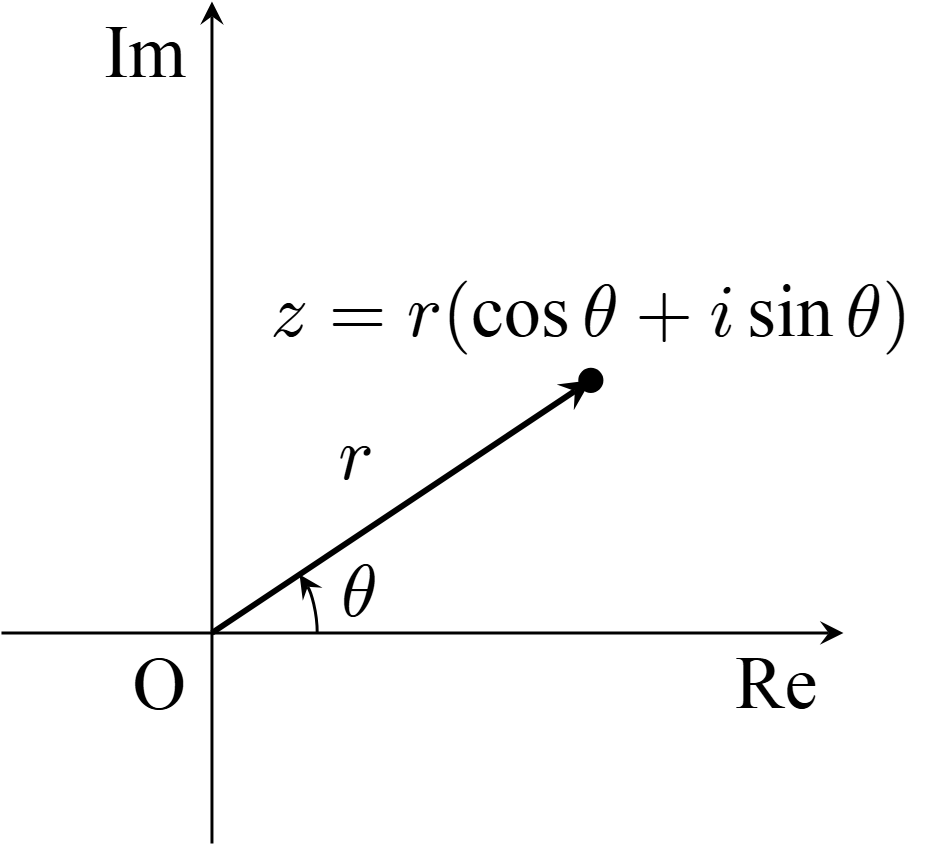
から
\[ z=r(\cos \theta +i\sin \theta )\]
となることが分かる．これを$z$の極形式(polar form)という．

複素数の極形式は，複素数の諸性質を直感的に理解するのに欠かせない．

複素数の加法と複素平面

以下，$z=a+bi\in \mathbb{C}$に対して，$\overrightarrow{z}=(a,b)\in \mathbb{R}^2$をベクトルとする．

$z=a+bi,w=c+di\in \mathbb{C}$に対して
\[ z+w=(a+c)+(b+d)i\]
であった．これは複素平面上で，ベクトルの和として理解することができる．

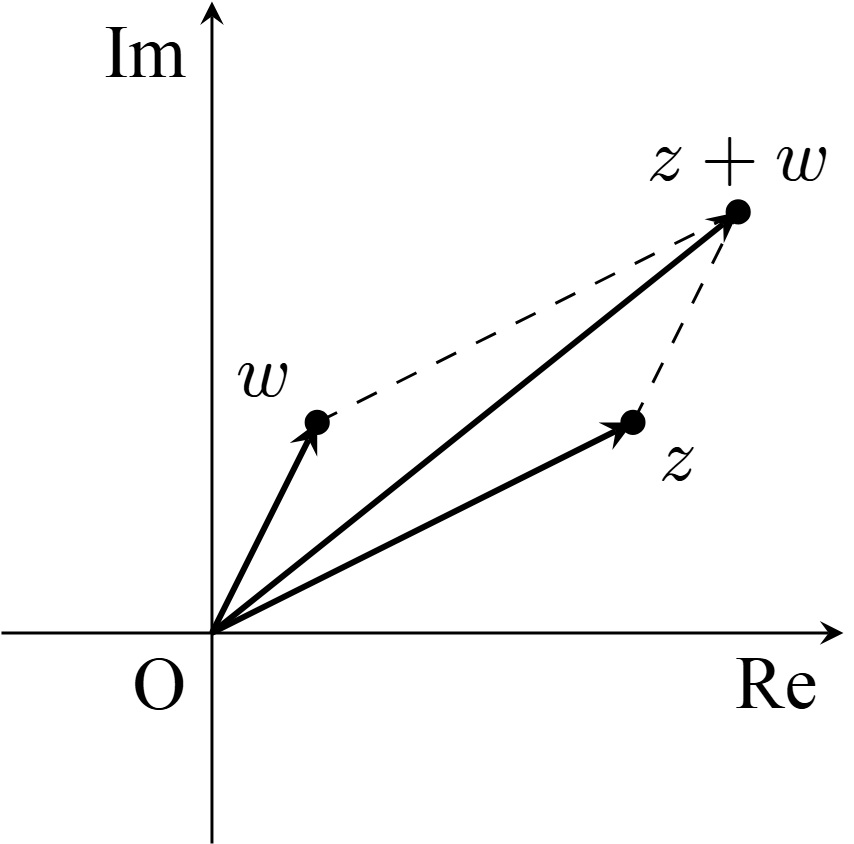
上図から
\[ \overrightarrow{z+w}=\overrightarrow{z}+\overrightarrow{w}\]
であることが分かる．

一方
\[ z-w=(a-c)+(b-d)i\]
は$z+(-w)$と考えることで，先程と同様にベクトルの和として理解することができる．

複素数の乗法と複素平面

$z=r_1(\cos \theta _1+i\sin \theta _1),w=r_2(\cos \theta _2+i\sin \theta _2)\in \mathbb{C}$に対して
\[ \begin{aligned}zw&=r_1r_2(\cos \theta _1+i\sin \theta _1)(\cos \theta _2+i\sin \theta _2)\\ &=r_1r_2((\cos \theta _1\cos \theta _2-\sin \theta _1\sin \theta _2)\\ &\quad +i(\sin \theta _1+\cos \theta _2+\cos \theta _1\sin \theta _2))\\ &=r_1r_2(\cos (\theta _1+\theta _2)+i\sin (\theta _1+\theta _2))\end{aligned}\]
であるから，$zw$は
\[ |zw|=|z||w|\\ \arg zw=\arg z+\arg w\]
を満たすことが分かる．

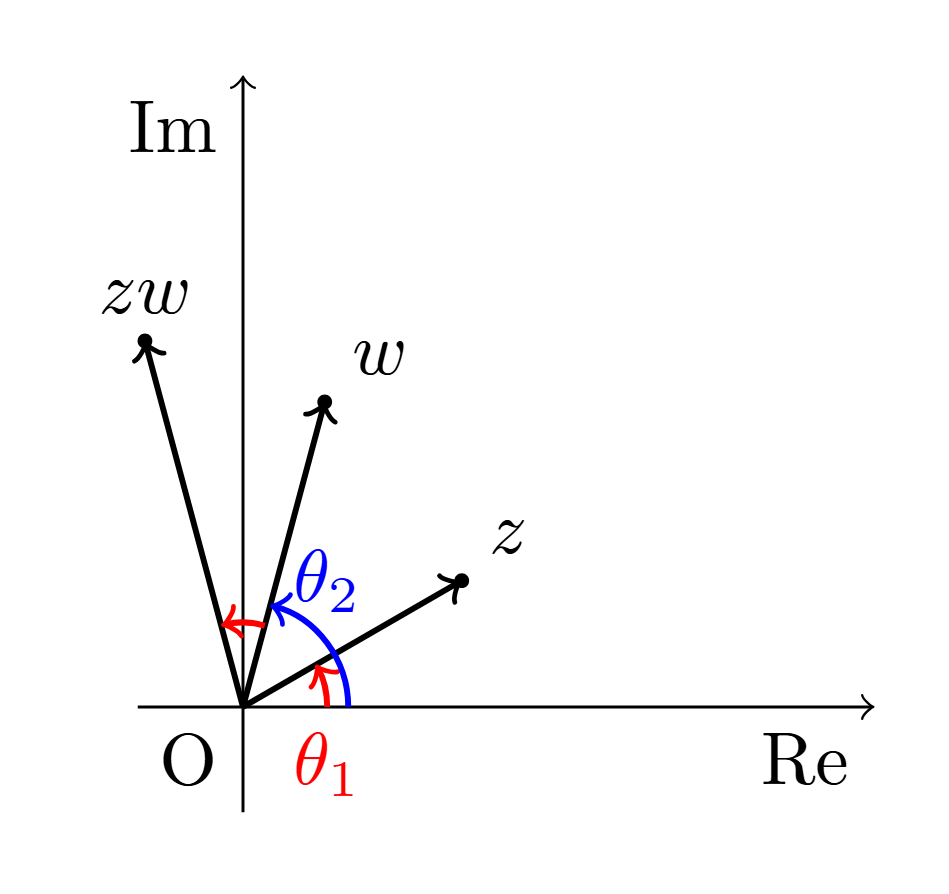
このように解釈すると，$z$は原点を中心とする$r_1$倍の拡大と角$\theta_1$の回転を表す複素数であると言える．

一方，$w\neq 0$であるとき
\[ \begin{aligned}\frac{1}{w}&=\frac{1}{r_2(\cos \theta _2+i\sin \theta _2)}\\ &=\frac{\cos \theta _2-i\sin \theta _2}{r_2(\cos \theta _2+i\sin \theta _2)(\cos \theta _2-i\sin \theta _2)}\\ &=\frac{\cos (-\theta _2)+i\sin (-\theta _2)}{r_2(\cos ^2\theta _2+\sin ^2\theta _2)}\\ &=\frac{1}{r_2}(\cos (-\theta _2)+i\sin (-\theta _2))\end{aligned}\]
であるから，$z$と$\dfrac{1}{w}$の積と考えることで
\[ \frac{z}{w}=\frac{r_1}{r_2}(\cos (\theta _1-\theta _2)+i\sin (\theta _1-\theta _2))\]
を得る．

共役複素数と複素平面

$z=a+bi=r(\cos \theta +i\sin \theta )\in \mathbb{C}$に対して
\[ \begin{aligned}\overline{z}&=a-bi=r(\cos \theta -i\sin \theta )\\ &=r(\cos (-\theta )+i\sin (-\theta ))\end{aligned}\]
は複素平面上で，実軸に関する対称移動として理解することができる．

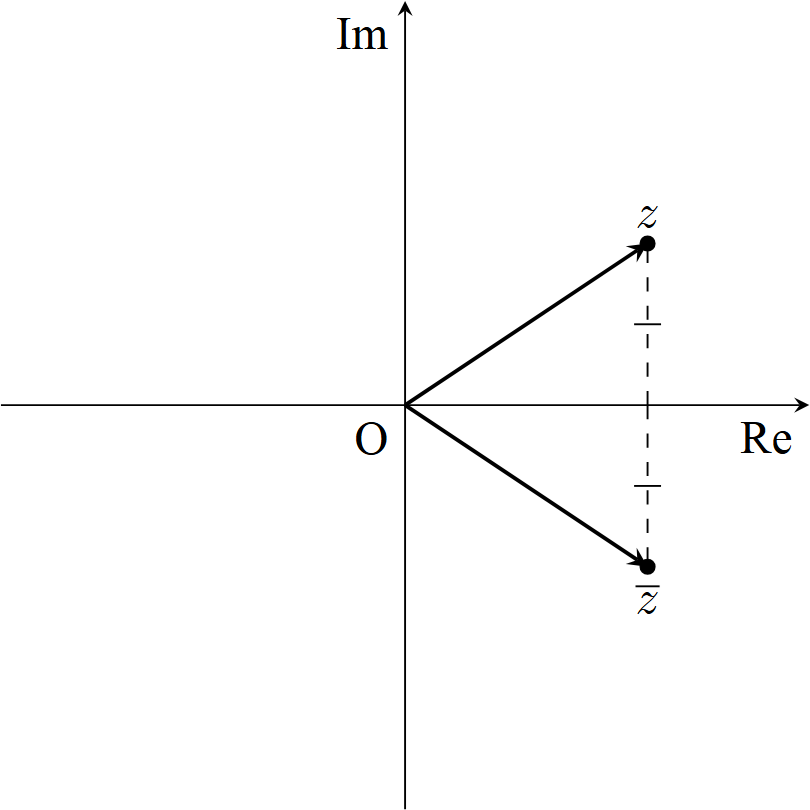
これを踏まえると，共役複素数についての諸性質を直感的に理解することができる．

1. $\arg$は$\mathbb{C}$から$\mathbb{R}$への多価関数(multivalued function)である．すなわち，$\arg z$の値は一意に定まらない．
   そこで，$\arg$の像$\mathbb{R}$を$[0,2\pi )$や$(-\pi ,\pi]$に制限し，偏角を一意に定めることがある． ↩︎