2階の導関数を調べることにより,関数のグラフの概形を掴もう.
凸関数と凹関数
関数の凹凸は,次のように厳密に定義される.
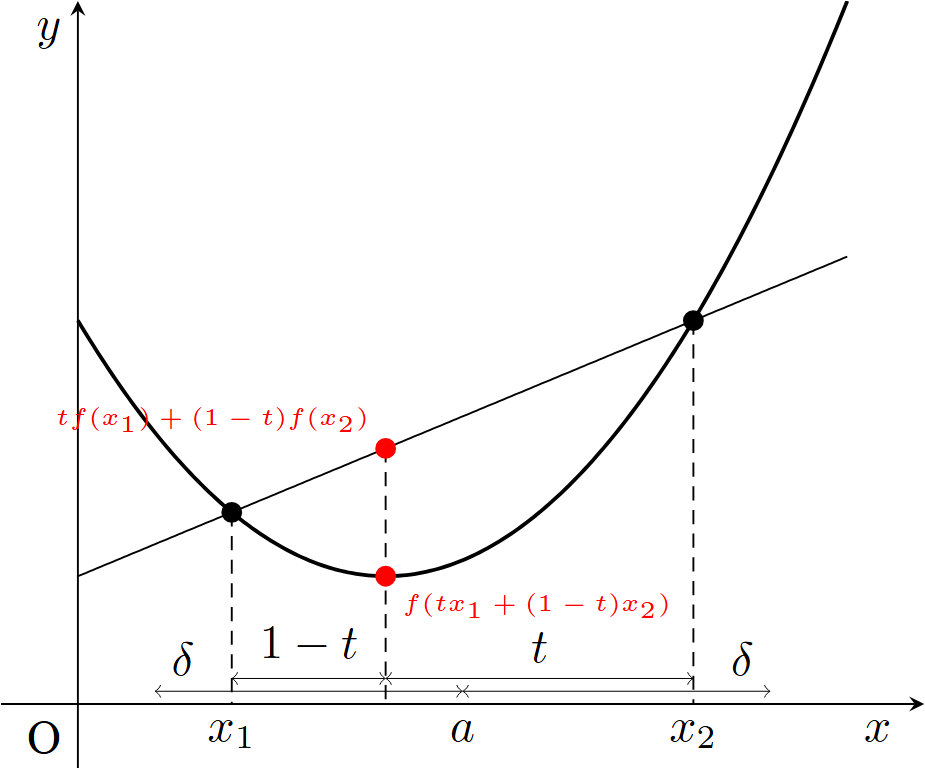
$I\subset \mathbb{R}$を開区間,$f:I\to \mathbb{R}$を関数とする.
- $a\in I$とする.ある$\delta >0$が存在し,任意の$x_1,x_2\in (a-\delta ,a+\delta )$と任意の$t\in [0,1]$に対して
\[ f(tx_1+(1-t)x_2)\le tf(x_1)+(1-t)f(x_2)\]
が成り立つとき,$f$は$x=a$で凸(または下に凸)(convex)であるという. - 任意の$a\in I$に対して,$f$が$x=a$で凸であるとき,$f$を凸関数(または下に凸な関数)(convex function)という.
- $a\in I$とする.ある$\delta >0$が存在し,任意の$x_1,x_2\in (a-\delta ,a+\delta )$と任意の$t\in (0,1)$に対して,$x_1\neq x_2$ならば
\[ f(tx_1+(1-t)x_2)<tf(x_1)+(1-t)f(x_2)\]
が成り立つとき,$f$は$x=a$で狭義の凸(または狭義の下に凸)(strictly convex)であるという. - 任意の$a\in I$に対して,$f$が$x=a$で狭義の凸であるとき,$f$を狭義の凸関数(または狭義の下に凸な関数)(strictly convex function)という.
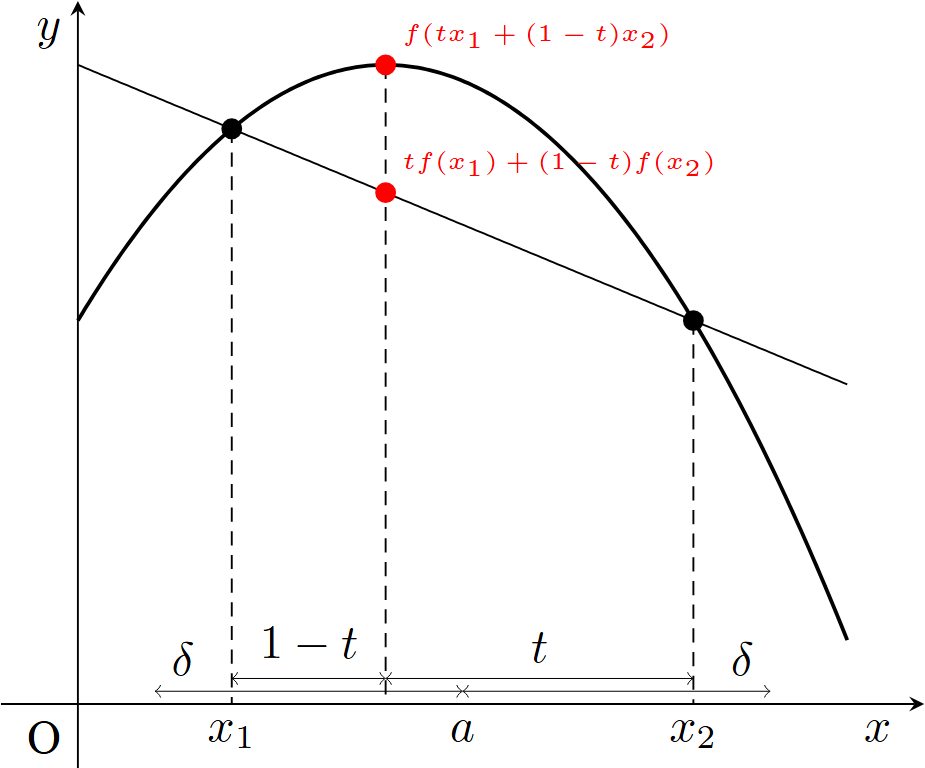
$I\subset \mathbb{R}$を開区間,$f:I\to \mathbb{R}$を関数とする.
- $a\in I$とする.ある$\delta >0$が存在し,任意の$x_1,x_2\in (a-\delta ,a+\delta )$と任意の$t\in [0,1]$に対して
\[ f(tx_1+(1-t)x_2)\ge tf(x_1)+(1-t)f(x_2)\]
が成り立つとき,$f$は$x=a$で凹(または上に凸)(concave)であるという. - 任意の$a\in I$に対して,$f$が$x=a$で凹であるとき,$f$を凹関数(または上に凸な関数)(concave function)という.
- $a\in I$とする.ある$\delta >0$が存在し,任意の$x_1,x_2\in (a-\delta ,a+\delta )$と任意の$t\in (0,1)$に対して,$x_1\neq x_2$ならば
\[ f(tx_1+(1-t)x_2)>tf(x_1)+(1-t)f(x_2)\]
が成り立つとき,$f$は$x=a$で狭義の凹(または狭義の上に凸)(strictly concave)であるという. - 任意の$a\in I$に対して,$f$が$x=a$で狭義の凹であるとき,$f$を狭義の凹関数(または狭義の上に凸な関数)(strictly concave function)という.
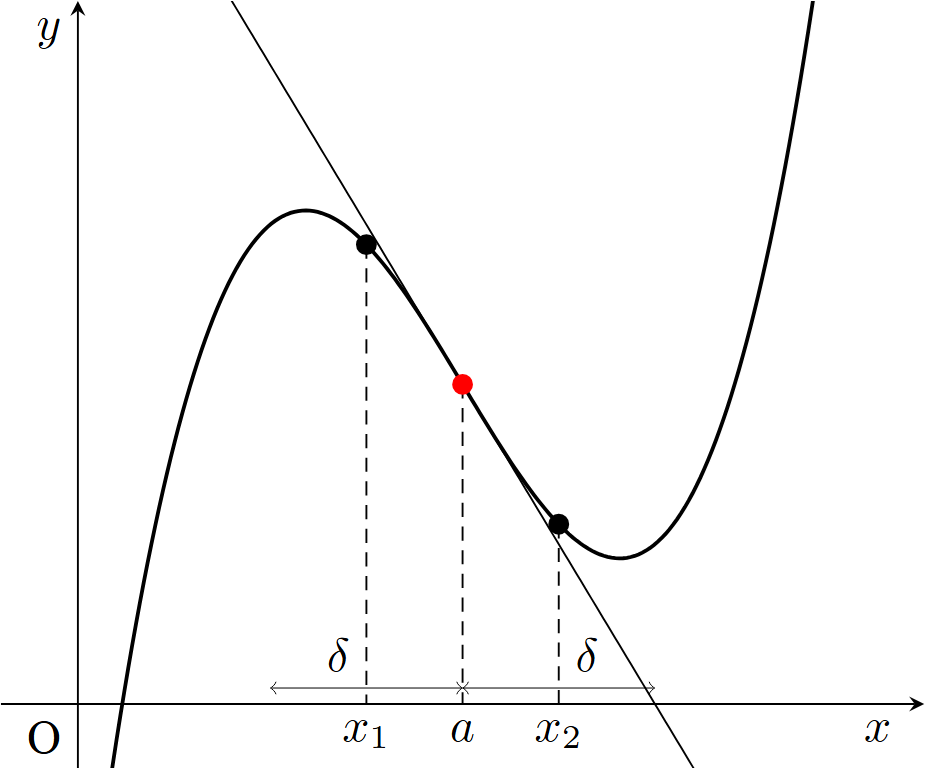
関数のグラフを考えるとき,次の概念も重要である.
$I\subset \mathbb{R}$を開区間,$f:I\to \mathbb{R}$を関数,$a\in I$とする.
ある$\delta >0$が存在して,任意の$x_1\in (a-\delta ,a)$と任意の$x_2\in (a,a+\delta )$に対して,$f$は$x=x_1$で凸かつ$x=x_2$で凹であるか,$f$は$x=x_1$で凹かつ$x=x_2$で凸であるとき,$(a,f(a))$は曲線$y=f(x)$の変曲点(inflection point, point of inflection, flex, inflection, inflexion)という.
2階の導関数と関数の凹凸
関数の凹凸は2回微分することによって判別することができる.
$I\subset \mathbb{R}$を開区間,$f:I\to \mathbb{R}$を$I$上$2$回微分可能である関数,$a\in I$とし,$f^{\prime \prime}(x)$は$x=a$で連続であるとする.
- $f^{\prime \prime}(a)>0$ならば,$f(x)$は$x=a$で凸である.
- $f^{\prime \prime}(a)<0$ならば,$f(x)$は$x=a$で凹である.
- $f^{\prime \prime}(a)=0$であり,ある$\delta >0$が存在して,任意の$x_1\in (a-\delta ,a)$と任意の$x_2\in (a,a+\delta )$に対して,$f^{\prime \prime}(x_1)f^{\prime \prime}(x_2)<0$となるならば,$(a,f(a))$は曲線$y=f(x)$の変曲点である.
- $f^{\prime \prime}(a)>0$より,ある$\delta >0$が存在して,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)$は狭義単調増加である.
$x_1<x_2$を満たす$x_1,x_2\in (a-\delta ,a+\delta )$に対して,関数$g:[0,1]\to \mathbb{R}$を
\[ g(t)=tf(x_1)+(1-t)f(x_2)-f(tx_1+(1-t)x_2)\quad (t\in [0,1])\]
により定めると
\[ g^{\prime}(t)=f(x_1)-f(x_2)-(x_1-x_2)f^{\prime}(tx_1+(1-t)x_2)\]
である.
$tx_1+(1-t)x_2\in (a-\delta ,a+\delta )$であることに注意すると,$g^{\prime}(t)$は狭義単調増加であるから,$g^{\prime \prime}(t)>0$
したがって
\[ f(tx_1+(1-t)x_2)<tf(x_1)+(1-t)f(x_2)\]
が成り立つから,$f$は$x=a$で凸である.$\blacksquare$ - $f^{\prime \prime}(a)<0$より,ある$\delta >0$が存在して,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)$は狭義単調減少である.
$x_1<x_2$を満たす$x_1,x_2\in (a-\delta ,a+\delta )$に対して,関数$g:[0,1]\to \mathbb{R}$を
\[ g(t)=tf(x_1)+(1-t)f(x_2)-f(tx_1+(1-t)x_2)\quad (t\in [0,1])\]
により定めると
\[ g^{\prime}(t)=f(x_1)-f(x_2)-(x_1-x_2)f^{\prime}(tx_1+(1-t)x_2)\]
である.
$tx_1+(1-t)x_2\in (a-\delta ,a+\delta )$であることに注意すると,$g^{\prime}(t)$は狭義単調減少であるから,$g^{\prime \prime}(t)<0$
したがって
\[ f(tx_1+(1-t)x_2)>tf(x_1)+(1-t)f(x_2)\]
が成り立つから,$f$は$x=a$で凹である.$\blacksquare$ - $f^{\prime \prime}(x_1)>0$かつ$f^{\prime \prime}(x_2)<0$であるとき,(1)及び(2)より,$f$は$x=x_1$で凸であり,$x=x_2$で凹であるから,$(a,f(a))$は曲線$y=f(x)$の変曲点である.
$f^{\prime \prime}(x_1)<0$かつ$f^{\prime \prime}(x_2)>0$であるとき,(1)及び(2)より,$f$は$x=x_1$で凹であり,$x=x_2$で凸であるから,$(a,f(a))$は曲線$y=f(x)$の変曲点である.$\blacksquare$
2階の導関数と極値
2階の導関数を用いることで,極値の判別がさらに容易になる.
$I\subset \mathbb{R}$を開区間,$f:I\to \mathbb{R}$を$I$上$2$回微分可能である関数,$a\in I$とし,$f^{\prime}(a)=0$かつ$f^{\prime \prime}(x)$は$x=a$で連続であるとする.
- $f^{\prime \prime}(a)>0$ならば,$f(a)$は$f(x)$の$x=a$における極小値である.
- $f^{\prime \prime}(a)<0$ならば,$f(a)$は$f(x)$の$x=a$における極大値である.
- $f^{\prime \prime}(a)=0$であり,ある$\delta >0$が存在して,任意の$x_1\in (a-\delta ,a)$と任意の$x_2\in (a,a+\delta )$に対して,$f^{\prime \prime}(x_1)f^{\prime \prime}(x_2)<0$となるならば,$f(a)$は$f(x)$の$x=a$における極値でない.
- $f^{\prime \prime}(a)>0$より,ある$\delta >0$が存在して,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)$は狭義単調増加である.
よって
\[ f^{\prime}(a)\begin{cases}<0&(a-\delta <x<a)\\ =0&(x=a)\\ >0&(a<x<a+\delta )\end{cases}\]
であるから,任意の$x\in (a-\delta ,a)$に対して$f(x)$は狭義単調減少であり,任意の$x\in (a,a+\delta )$に対して$f(x)$は狭義単調増加である.
したがって,$f(a)$は$f(x)$の$x=a$における極小値である.$\blacksquare$ - $f^{\prime \prime}(a)<0$より,ある$\delta >0$が存在して,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)$は狭義単調減少である.
よって
\[ f^{\prime}(a)\begin{cases}>0&(a-\delta <x<a)\\ =0&(x=a)\\ <0&(a<x<a+\delta )\end{cases}\]
であるから,任意の$x\in (a-\delta ,a)$に対して$f(x)$は狭義単調増加であり,任意の$x\in (a,a+\delta )$に対して$f(x)$は狭義単調減少である.
したがって,$f(a)$は$f(x)$の$x=a$における極大値である.$\blacksquare$ - $f^{\prime \prime}(x_1)>0$かつ$f^{\prime \prime}(x_2)<0$であるとき,任意の$x\in (a-\delta ,a)$に対して$f^{\prime}(x)$は狭義単調増加であり,任意の$x\in (a,a+\delta )$に対して$f^{\prime}(x)$は狭義単調減少であるから,$f^{\prime}(a)=0$より,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)\le 0$すなわち$f$は広義単調減少であるから,$f(a)$は$f(x)$の$x=a$における極値でない.
$f^{\prime \prime}(x_1)<0$かつ$f^{\prime \prime}(x_2)>0$であるとき,任意の$x\in (a-\delta ,a)$に対して$f^{\prime}(x)$は狭義単調減少であり,任意の$x\in (a,a+\delta )$に対して$f^{\prime}(x)$は狭義単調増加であるから,$f^{\prime}(a)=0$より,任意の$x\in (a-\delta ,a+\delta )$に対して,$f^{\prime}(x)\ge 0$すなわち$f$は広義単調増加であるから,$f(a)$は$f(x)$の$x=a$における極値でない.$\blacksquare$

