位相空間論が発展した歴史とともに,位相空間や距離空間を定義する動機や直感的イメージをまとめた.
$\mathbb{R}$の性質
実数全体の集合$\mathbb{R}$は,数直線を用いることで可視化することができた.
まず,1つの実数は直線上の1点と1対1に対応付けることができる.すなわち,直線上の点全体の集合を$S$とすると,全単射$f:\mathbb{R}\to S$がいくつか存在する.
次に,この全単射$f$を次を満たすように定める.
$x\in \mathbb{R}$,$\mathrm{O}=f(0),\mathrm{P}=f(x),Q=f(-x)$とする.
- $\rm Q$は$\rm O$に関して$\rm P$と対称な位置にある.
- 線分$\rm OP$の長さは$x$である.
$\mathbb{R}$上の距離
このとき,2つの実数の距離を定めることができる.まずはその準備として,絶対値を導入しておこう.
$x\in \mathbb{R}$とする.
$x$の絶対値(absolute value)(または母数(modulus))$|x|$を次のように定める.
\[ |x|=\begin{cases}x&(x\ge 0)\\ -x&(x<0)\end{cases}\]
この絶対値を用いることで,$\mathbb{R}$上に距離を定義することができる.
$x,y\in \mathbb{R}$とする.
写像$d:\mathbb{R}^2\to \mathbb{R}$を次のように定める.
\[ d(x,y)=|x-y|\quad (x,y\in \mathbb{R})\]
このとき,$d$を$\mathbb{R}$上のユークリッド距離(Euclidean distance)(またはユークリッド距離関数,ユークリッド計量(Euclidean metric))といい,$d(x,y)$を$x$と$y$の距離(distance)という.
このようにして定めた$\mathbb{R}$上の距離は,次の性質を満たす.
$x,y,z\in \mathbb{R}$,$d$を$\mathbb{R}$上のユークリッド距離とするとき,次が成り立つ.
- (正値性(positivity)) $d(x,y)=0$
等号成立条件は$x=y$ - (対称性(symmetry)) $d(x,y)=d(y,x)$
- (三角不等式(triangle inequality)) $d(x,z)\le d(x,y)+d(y,z)$
$\mathbb{R}$上の開集合
$\mathbb{R}$上に定義されたユークリッド距離を用いて定義される集合について考えよう.
$\varepsilon >0$,$a\in \mathbb{R}$とする.
$a$の$\varepsilon$近傍(neighborhood)を次のように定める.
\[ B_{\varepsilon}(a)=\{ x\in \mathbb{R}\mid d(x,a)<\varepsilon \} \]
すなわち,$a\in \mathbb{R}$の$\varepsilon>0$近傍は
\[ B_{\varepsilon}(a)=(a-\varepsilon ,a+\varepsilon )\]
という開区間を表している.数直線上で$a\pm \varepsilon$よりも$a$に近い実数全体の集合が$B_{\varepsilon}(a)$である.
これを用いて,$\mathbb{R}$の開集合を定義する.
$O\subset \mathbb{R}$とする.
任意の$a\in O$に対し,ある$\varepsilon >0$が存在し,$B_{\varepsilon}(a)\subset O$となるとき,$O$を$\mathbb{R}$の開集合(open set)という.
ただし,$\emptyset$は$\mathbb{R}$の開集合であると定める.
すなわち開集合とは,その任意の元$a$の$\varepsilon >0$近傍$B_{\varepsilon}(a)$について,$\varepsilon$を十分小さくすると,$B_{\varepsilon}(a)$全体が$O$の中にすっぽりと入るような集合のことである.

この開集合が持つ3つの性質を紹介する.この性質を簡潔に記述するために,次の集合を定義しておこう.
$\mathbb{R}$の開集合全体の集合族を$\mathbb{R}$の開集合系(open sets)といい,$\mathcal{O}$で表す.
$\mathbb{R}$の開集合系$\mathcal{O}$について,次が成り立つ.
- $\emptyset \in \mathcal{O}$かつ$\mathbb{R}\in \mathcal{O}$
- $O_1,O_2\in \mathcal{O}\implies O_1\cap O_2\in \mathcal{O}$
- $\{ O_{\lambda}\} _{\lambda \in \Lambda}$を$\Lambda$を添字集合とする集合族とする.
\[ \forall \lambda \in \Lambda ,O_{\lambda}\in \mathcal{O}\implies \bigcup _{\lambda \in \Lambda}O_{\lambda}\in \mathcal{O}\]
$\mathbb{R}^n$の性質
次に,$\mathbb{R}$を一般化して$\mathbb{R}^n$について考えることにしよう.$\mathbb{R}$は直線に対応付けることができたが,$\mathbb{R}^n$は$n$次元空間に対応付ける必要がある.
以下,$n\in \mathbb{N}$とする.$\mathbb{R}$の$n$個の直積である$n$次元ユークリッド空間$\mathbb{R}^n$は,$n$次元空間を用いて可視化することができた.
まず,1つの実数は$n$次元空間上の1点と1対1に対応付けることができる.すなわち,$n$次元空間上の点全体の集合を$S$とすると,全単射$f:\mathbb{R}^n\to S$がいくつか存在する.
次に,この全単射$f$を次を満たすように定める.
$\bm{x}=(x_1,x_2,\dots ,x_n)\in \mathbb{R}^n$,$\mathrm{O}=f(\bm{0}),\mathrm{P}=f(\bm{x}),Q=f(-\bm{x})$とする.
- $\rm Q$は$\rm O$に関して$\rm P$と対称な位置にある.
- $i$を$1$以上$n$以下の整数とする.線分$\rm OP$の第$i$座標は$\bm{x}$の第$i$成分$x_i$である.
$n=3$のとき,次のようになる.
$\mathbb{R}^n$上の距離
$\mathbb{R}^n$には,和とスカラー倍に加え,内積という演算が定義されている.
$\bm{x}=(x_1,x_2,\dots ,x_n),\bm{y}=(y_1,y_2,\dots ,y_n)\in \mathbb{R}^n$とする.
$\bm{x}$と$\bm{y}$の内積(inner product)(またはスカラー積(scalar product))$\bm{x}\cdot \bm{y}$を次のように定める.
\[ \bm{x}\cdot \bm{y}=x_1y_1+x_2y_2+\dots +x_ny_n\]
このとき,$\mathbb{R}^n$の2つの元の距離を定めることができる.まずはその準備として,ノルムを導入しておこう.
$\bm{x}\in \mathbb{R}^n$とする.
$\bm{x}$のノルム(norm)$\| \bm{x}\|$を次のように定める.
\[ \| \bm{x}\| =\sqrt{\bm{x}\cdot \bm{x}}=\sqrt{x_1^2+x_2^2+\dots +x_n^2}\]
このノルムを用いることで,$\mathbb{R}^n$上に距離を定義することができる.
$\bm{x},\bm{y}\in \mathbb{R}^n$とする.
写像$d:\mathbb{R}^n\times \mathbb{R}^n\to \mathbb{R}$を次のように定める.
\[ d(\bm{x},\bm{y})=\| \bm{x}-\bm{y}\| \quad (\bm{x},\bm{y}\in \mathbb{R}^n)\]
このとき,$d$を$\mathbb{R}^n$上のユークリッド距離(Euclidean distance)(またはユークリッド距離関数,ユークリッド計量(Euclidean metric))といい,$d(\bm{x},\bm{y})$を$\bm{x}$と$\bm{y}$の距離(distance)という.
このようにして定めた$\mathbb{R}^n$上の距離は,命題1と同様な次の性質を満たす.
$\bm{x},\bm{y},\bm{z}\in \mathbb{R}^n$,$d$を$\mathbb{R}^n$上のユークリッド距離とするとき,次が成り立つ.
- (正値性(positivity)) $d(\bm{x},\bm{y})\ge 0$
等号成立条件は$\bm{x}=\bm{y}$ - (対称性(symmetry)) $d(\bm{x},\bm{y})=d(\bm{y},\bm{x})$
- (三角不等式(triangle inequality)) $d(\bm{x},\bm{z})\le d(\bm{x},\bm{y})+d(\bm{y},\bm{z})$
$\mathbb{R}$上の開集合
$\mathbb{R}^n$上に定義されたユークリッド距離を用いて定義される集合について考えよう.
$\varepsilon >0$,$\bm{a}\in \mathbb{R}^n$とする.
$\bm{a}$の$\varepsilon$近傍(neighborhood)を次のように定める.
\[ B_{\varepsilon}(\bm{a})=\{ \bm{x}\in \mathbb{R}\mid d(\bm{x},\bm{a}) <\varepsilon \} \]
すなわち,$\bm{a}\in \mathbb{R}^n$の$\varepsilon>0$近傍$B_{\varepsilon}(\bm{a})$は,$n$次元空間上で$\bm{a}$を中心とする半径$\varepsilon$の$n$次元球体の内側(球面上は除く)にある元全体の集合である.
例えば,$n=3$のときは次のようになる.
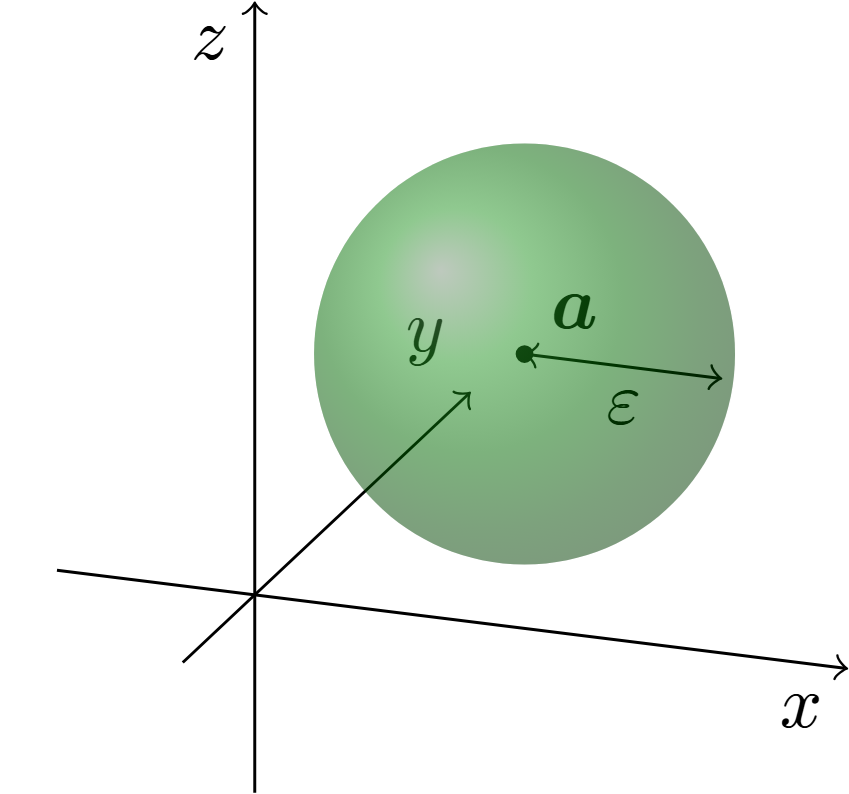
これを用いて,$\mathbb{R}^n$の開集合を定義する.
$O\subset \mathbb{R}^n$とする.
任意の$\bm{a}\in O$に対し,ある$\varepsilon >0$が存在し,$B_{\varepsilon}(\bm{a})\subset O$となるとき,$O$を$\mathbb{R}^n$の開集合(open set)という.
ただし,$\emptyset$は$\mathbb{R}^n$の開集合であると定める.
すなわち開集合とは,その任意の元$\bm{a}$の$\varepsilon >0$近傍$B_{\varepsilon}(\bm{a})$について,$\varepsilon$を十分小さくすると,$B_{\varepsilon}(\bm{a})$全体が$O$の中にすっぽりと入るような集合のことである.
例えば,$n=2$のときは次のようになる.
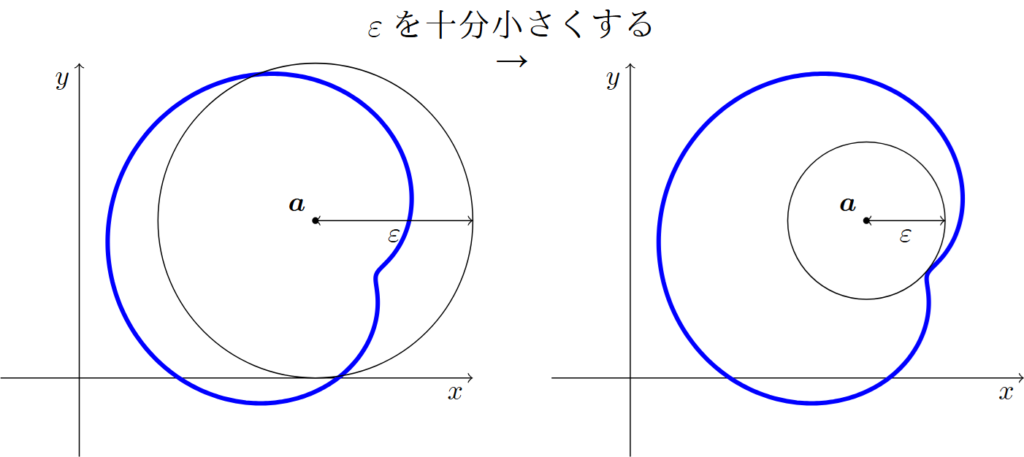
この開集合は命題2と同様の性質を持つ.この性質を簡潔に記述するために,次の集合を定義しておこう.
$\mathbb{R}^n$の開集合全体の集合族を$\mathbb{R}^n$の開集合系(open sets)といい,$\mathcal{O}$で表す.
$\mathbb{R}^n$の開集合系$\mathcal{O}$について,次が成り立つ.
- $\emptyset \in \mathcal{O}$かつ$\mathbb{R}^n\in \mathcal{O}$
- $O_1,O_2\in \mathcal{O}\implies O_1\cap O_2\in \mathcal{O}$
- $\{ O_{\lambda}\} _{\lambda \in \Lambda}$を$\Lambda$を添字集合とする集合族とする.
\[ \forall \lambda \in \Lambda ,O_{\lambda}\in \mathcal{O}\implies \bigcup _{\lambda \in \Lambda}O_{\lambda}\in \mathcal{O}\]
距離空間
次に,$\mathbb{R}^n$を一般化した距離空間について考えることにしよう.$\mathbb{R}^n$は$n$次元空間に対応付け,ユークリッド距離を導入することで開集合を定義した.しかし,距離には様々な種類がある.$\mathbb{R}^n$では,マンハッタン距離やチェビシェフ距離などといったユークリッド距離とは異なる距離について考えることもできる.
そこで,このような距離の概念を一般化して,一般の集合に対して距離という概念を導入することを考えてみよう.
距離空間の定義
一般の集合に対して距離を定めるには,距離の定義を明確にしておく必要がある.
そこで,$\mathbb{R}$や$\mathbb{R}^n$のユークリッド距離が満たしていた性質である命題1や命題3に注目し,逆にそのような性質を持つ写像$d$を「距離」と呼ぶことにしよう.
$X$を空でない集合とする.
任意の$x,y,z\in X$に対し,写像$d:X\times X\to \mathbb{R}$が次の3つの性質をすべて満たすとき,$d$を$X$の距離関数(または距離)といい,$d(x,y)$を$x$と$y$の距離という.
- (正値性(positivity)) $d(x,y)\ge 0$
等号成立条件は$x=y$ - (対称性(symmetry)) $d(x,y)=d(y,x)$
- (三角不等式(triangle inequality)) $d(x,z)\le d(x,y)+d(y,z)$
このとき,$X$を距離空間(metric space)といい,$X$を$(X,d)$とも表す.
今までの流れは
距離関数の定義 → 距離関数の3性質
という論理になっていたが,一般の距離関数を定義するために
距離関数の3性質 → 距離関数の定義
という逆の論理構成になっていることに注意が必要である.距離関数の3性質を距離空間の公理と捉えたのである.
距離空間上の開集合
$\mathbb{R}$や$\mathbb{R}^n$のユークリッド距離に対して開集合を定義したのと同様に,距離空間における開集合を定義しよう.
$(X,d)$を距離空間,$\varepsilon >0$,$a\in X$とする.
$a$の$\varepsilon$近傍(neighborhood)を次のように定める.
\[ B_{\varepsilon}(a)=\{ x\in \mathbb{R}\mid d(x,a) <\varepsilon \} \]
すなわち,$a\in X$の$\varepsilon>0$近傍$B_{\varepsilon}(\bm{a})$は,距離関数$d$が定められた距離空間$X$上で$a$を中心とする半径$\varepsilon$の球体の内側(球面上は除く)にある元全体の集合である.
これを用いて,距離空間の開集合を定義する.
$X$を距離空間とする.$O\subset X$とする.
任意の$a\in O$に対し,ある$\varepsilon >0$が存在し,$B_{\varepsilon}(a)\subset O$となるとき,$O$を$X$の開集合(open set)という.
ただし,$\emptyset$は$X$の開集合であると定める.
すなわち開集合とは,その任意の元$a$の$\varepsilon >0$近傍$B_{\varepsilon}(a)$について,$\varepsilon$を十分小さくすると,$B_{\varepsilon}(a)$全体が$O$の中にすっぽりと入るような集合のことである.
この開集合は命題2や命題4と同様の性質を持つ.この性質を簡潔に記述するために,次の集合を定義しておこう.
距離空間$X$の開集合全体の集合族を$X$の開集合系(open sets)といい,$\mathcal{O}$で表す.
距離空間$X$の開集合系$\mathcal{O}$について,次が成り立つ.
- $\emptyset \in \mathcal{O}$かつ$X\in \mathcal{O}$
- $O_1,O_2\in \mathcal{O}\implies O_1\cap O_2\in \mathcal{O}$
- $\{ O_{\lambda}\} _{\lambda \in \Lambda}$を$\Lambda$を添字集合とする集合族とする.
\[ \forall \lambda \in \Lambda ,O_{\lambda}\in \mathcal{O}\implies \bigcup _{\lambda \in \Lambda}O_{\lambda}\in \mathcal{O}\]
位相空間
いよいよ,距離空間までをも一般化した位相空間について考えることにしよう.
距離空間は,$\mathbb{R}$や$\mathbb{R}^n$のユークリッド距離を一般化して,一般の集合に対して一般の距離関数を導入することで開集合などを定義した.
位相空間では,距離関数が定められていない一般の集合に対しても,開集合の定義を可能にする.
位相空間の定義
一般の集合に対して開集合を定めるには,開集合の定義を明確にしておく必要がある.
そこで,$\mathbb{R}$や$\mathbb{R}^n$,距離空間$(X,d)$の開集合が満たしていた性質である命題2や命題4,命題5に注目し,逆にそのような性質を持つ集合族$\mathcal{O}$の元を「開集合」と呼ぶことにしよう.
$X$を空でない集合とする.
$X$の部分集合族$\mathcal{O}$が次の3つの性質をすべて満たすとき,$\mathcal{O}$を$X$の位相(topology)(または開集合系(open sets))といい,$\mathcal{O}$の元を開集合(open set)という.
- $\emptyset \in \mathcal{O}$かつ$X\in \mathcal{O}$
- $O_1,O_2\in \mathcal{O}\implies O_1\cap O_2\in \mathcal{O}$
- $\{ O_{\lambda}\} _{\lambda \in \Lambda}$を$\Lambda$を添字集合とする集合族とする.
\[ \forall \lambda \in \Lambda ,O_{\lambda}\in \mathcal{O}\implies \bigcup _{\lambda \in \Lambda}O_{\lambda}\in \mathcal{O}\]
このとき,$X$を位相空間(topological space)といい,$X$を$(X,\mathcal{O})$とも表す.
今までの流れは
開集合の定義 → 開集合系の3性質
という論理になっていたが,一般の距離関数を定義するために
開集合系の3性質 → 開集合の定義
という逆の論理構成になっていることに注意が必要である.開集合系の3性質を位相空間の公理と捉えたのである.
位相空間を考える意義
数学では異なるものの共通点を発見し,それをもとに一般化した概念を考えることで,それらを同一視し,統一的に扱うことができるようになる.
位相空間では,一般の開集合を定義している.集合$X$とその部分集合族$\mathcal{O}$について考えているとき,もしも$\mathcal{O}$が$X$の位相であるならば,位相空間の性質を用いて議論を進めることができるようになる.
数学ではしばしば「空間」という用語が用いられている.数学における空間の定義は明確なものではないが,集合にある種の構造を入れたものを「空間」と読んでいる.
例えば,位相空間は「位相空間の3つの公理」という構造を集合に導入したものであり,ベクトル空間は「ベクトルの和とスカラー倍」という構造を集合に導入したものである.このような構造を持って,一見異なる対象も同一視することができるようになるのである.
位相空間論は多様体や数直線の部分集合,内積空間に関する研究によって発展してきた分野である.抽象度の高い数学ではあるが,数学を記述し,議論するために必要不可欠な内容である.

