数列の単調性

数列の項の特徴として，その大小関係を考えることは非常に有効である．ここでは数列の単調性についての定義をまとめた．

数列の単調性

数列の単調性

数列の単調性は，次の4つに分類できる．

狭義単調増加	$\forall n\in \mathbb{N},a_n<a_{n+1}$
狭義単調減少	$\forall n\in \mathbb{N},a_n>a_{n+1}$
広義単調増加	$\forall n\in \mathbb{N},a_n\le a_{n+1}$
広義単調減少	$\forall n\in \mathbb{N},a_n\ge a_{n+1}$

以下，それぞれの定義と例を挙げ，詳細に解説する．

狭義単調増加数列

定義1

任意の$n\in \mathbb{N}$に対し，$a_n<a_{n+1}$が成り立つ数列$\{ a_n\} _{n=1}^{\infty}$を狭義単調増加数列(または狭義単調増加列(strictly monotonically increasing sequence)，狭義増加数列(または狭義増加列)(strictly increasing sequence))といい，$\{ a_n\} _{n=1}^{\infty}$は狭義単調増加(strictly monotonically increasing)(または狭義増加(strictly increasing))であるという．

例1

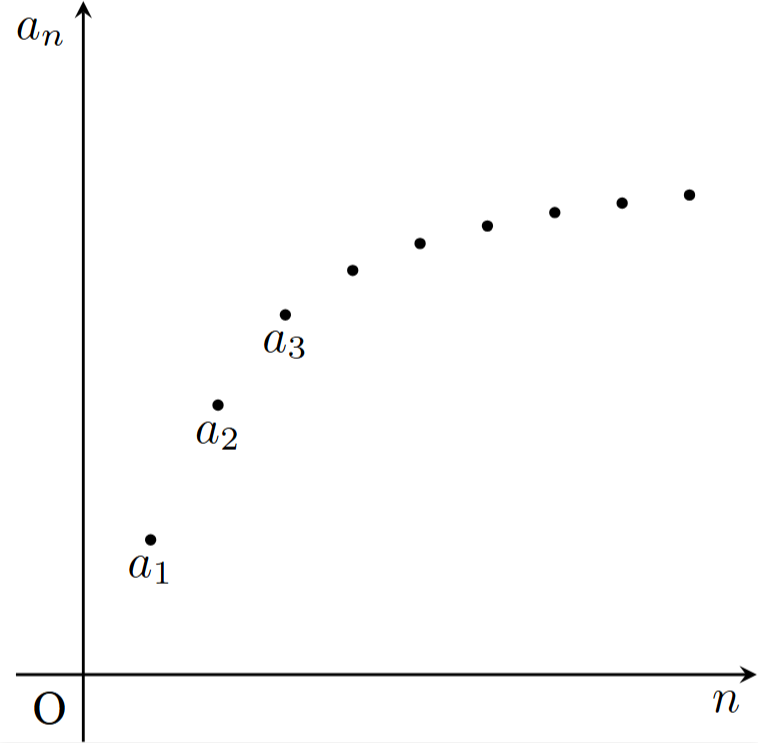
数列$\{ a_n\} _{n=1}^{\infty}$を
\[ a_n=n+\frac{1}{n}\quad (n\in \mathbb{N})\]
により定めると，任意の$n\in \mathbb{N}$に対し
\[ a_n=n+\frac{1}{n}<n+1+\frac{1}{n+1}=a_{n+1}\]
が成り立つから，$\{ a_n\} _{n=1}^{\infty}$は狭義単調増加数列である．

狭義単調減少数列

定義2

任意の$n\in \mathbb{N}$に対し，$a_n>a_{n+1}$が成り立つ数列$\{ a_n\} _{n=1}^{\infty}$を狭義単調減少数列(または狭義単調減少列(strictly monotonically decreasing sequence)，狭義減少数列(または狭義減少列)(strictly decreasing sequence))といい，$\{ a_n\} _{n=1}^{\infty}$は狭義単調減少(strictly monotonically decreasing)(または狭義減少(strictly decreasing))であるという．

例2

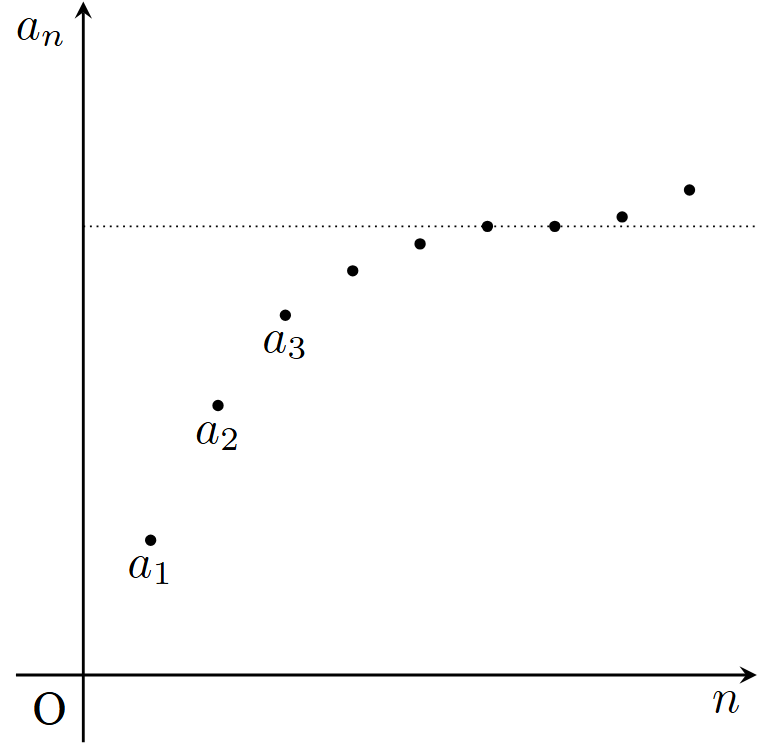
数列$\{ a_n\} _{n=1}^{\infty}$を
\[ a_n=\frac{1}{n-1}-\frac{1}{n+1}\quad (n\in \mathbb{N})\]
により定めると，任意の$n\in \mathbb{N}$に対し
\[ a_n=\frac{1}{n-1}-\frac{1}{n+1}=\frac{2}{n^2-1}>\frac{2}{n^2+2n}<\frac{1}{n}-\frac{1}{n+2}=a_{n+1}\]
が成り立つから，$\{ a_n\} _{n=1}^{\infty}$は狭義単調減少数列である．

広義単調増加数列

定義3

任意の$n\in \mathbb{N}$に対し，$a_n\le a_{n+1}$が成り立つ数列$\{ a_n\} _{n=1}^{\infty}$を広義単調増加数列(または広義単調増加列(weakly monotonically increasing sequence)，広義増加数列(または広義増加列)(weakly increasing sequence))といい，$\{ a_n\} _{n=1}^{\infty}$は広義単調増加(weakly monotonically increasing)(または広義増加(weakly increasing)，非減少(non-decreasing))であるという．

例3

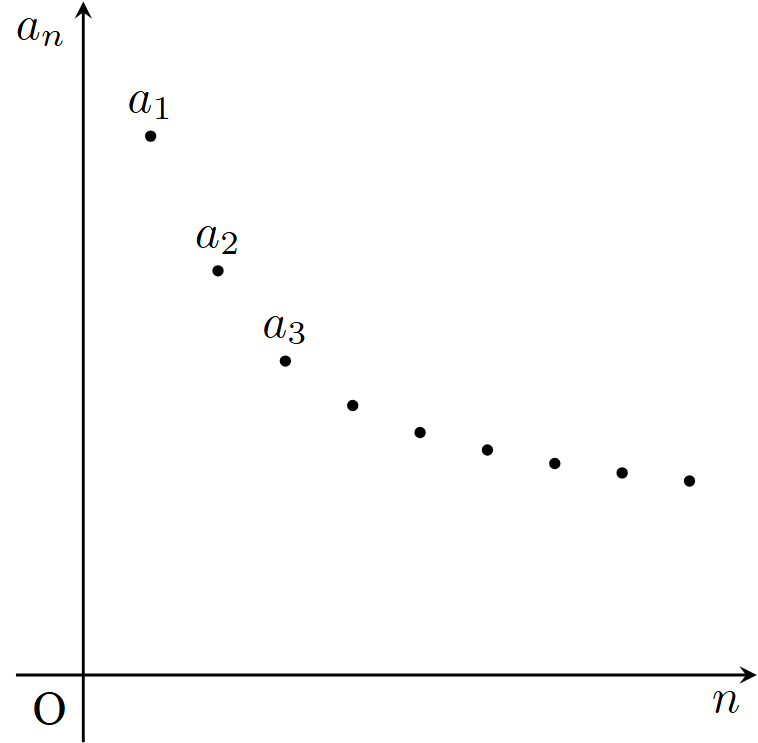
数列$\{ a_n\} _{n=1}^{\infty}$を
\[ a_n=[\sqrt{n}]=\max \{ x\in \mathbb{Z}\mid x\le \sqrt{n}\} \quad (n\in \mathbb{N})\]
により定めると¹，任意の$n\in \mathbb{N}$に対し
\[ \sqrt{n}<\sqrt{n+1}\]
より
\[ a_n=[\sqrt{n}]\le [\sqrt{n+1}]=a_{n+1}\]
が成り立つから，$\{ a_n\} _{n=1}^{\infty}$は広義単調増加数列である．

広義単調減少数列

定義4

任意の$n\in \mathbb{N}$に対し，$a_n\ge a_{n+1}$が成り立つ数列$\{ a_n\} _{n=1}^{\infty}$を広義単調減少数列(または広義単調減少列(weakly monotonically decreasing sequence)，広義減少数列(または広義減少列)(weakly decreasing sequence))といい，$\{ a_n\} _{n=1}^{\infty}$は広義単調減少(weakly monotonically decreasing)(または広義減少(weakly decreasing)，非増加(non-increasing))であるという．

例4

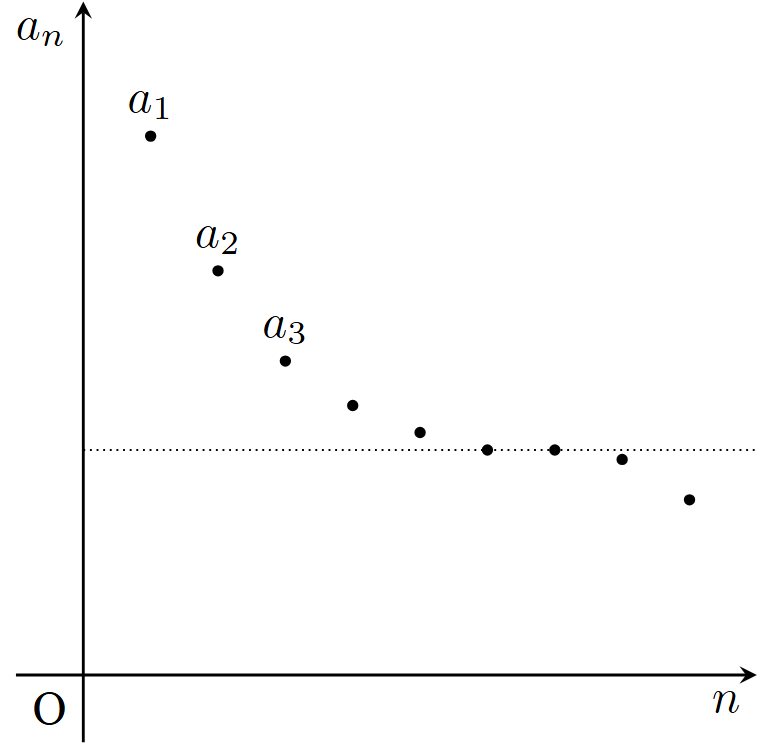
数列$\{ a_n\} _{n=1}^{\infty}$を
\[ a_n=\begin{cases}-n&(nは奇数)\\ -n-1&(nは偶数)\end{cases}\quad (n\in \mathbb{N})\]
により定めると，任意の$n\in \mathbb{N}$に対し
\[ a_n\ge -n-1\ge a_{n+1}\]
が成り立つから，$\{ a_n\} _{n=1}^{\infty}$は広義単調減少数列である．

文脈によって｢狭義｣か｢広義｣かが明らかなときは，これを省略することがある．当サイトでは混同を避けるため，｢高校数学｣カテゴリーの記事など一部を除いて｢狭義｣及び｢広義｣を省略せずに表現することにしている．

数列が単調増加または単調減少である性質を数列の単調性(monotonicity)という．

数列の単調性と収束性には密接な関係がある．これについては以下の記事で詳しく解説している．