この記事に誤植の可能性のある記述を見つけた場合，お問合せフォームからご連絡ください．

区間 ～定義･イメージ･例を解説～

real_intervalこの記事のPDFファイルのダウンロード･印刷はこちらから

区間とは，数直線の一部分を表す集合のことです．

区間とは

$a,b\in \mathbb{R}$とする．
$a\le b$のとき
\[ [a,b]=\{ x\in \mathbb{R}\mid a\le x\le b\} \]
を有界閉区間(bounded closed interval)という．
$a<b$のとき
\[ (a,b)=\{ x\in \mathbb{R}\mid a<x<b\} \]
を有界開区間(bounded open interval)といい，
\[ [a,b)=\{ x\in \mathbb{R}\mid a\le x<b\} \]
\[ (a,b]=\{ x\in \mathbb{R}\mid a<x\le b\} \]
を半開区間(half-open interval)という．
また
\[ [a,+\infty )=\{ x\in \mathbb{R}\mid x\ge a\} \]
\[ (-\infty ,a]=\{ x\in \mathbb{R}\mid x\le a\} \]
を無限閉区間(infinite closed interval)(または非有界閉区間(unbounded closed interval))といい，
\[ (a,+\infty )=\{ x\in \mathbb{R}\mid x>a\} \]
\[ (-\infty ,a)=\{ x\in \mathbb{R}\mid x<a\} \]
を無限開区間(infinite open interval)(または非有界開区間(unbounded open interval))という．
特に，$\mathbb{R}=(-\infty ,+\infty )$であり，これらを総称して区間(interval)(または実区間(real interval))という．

区間の定義

区間の厳密な定義は次のようになる．

定義1

$a,b\in \mathbb{R}$とする．
$a\le b$のとき
\[ [a,b]=\{ x\in \mathbb{R}\mid a\le x\le b\} \]
を有界閉区間(bounded closed interval)という．
$a<b$のとき
\[ (a,b)=\{ x\in \mathbb{R}\mid a<x<b\} \]
を有界開区間(bounded open interval)といい，
\[ [a,b)=\{ x\in \mathbb{R}\mid a\le x<b\} \]
\[ (a,b]=\{ x\in \mathbb{R}\mid a<x\le b\} \]
を半開区間(half-open interval)という．
また
\[ [a,+\infty )=\{ x\in \mathbb{R}\mid x\ge a\} \]
\[ (-\infty ,a]=\{ x\in \mathbb{R}\mid x\le a\} \]
を無限閉区間(infinite closed interval)(または非有界閉区間(unbounded closed interval))といい，
\[ (a,+\infty )=\{ x\in \mathbb{R}\mid x>a\} \]
\[ (-\infty ,a)=\{ x\in \mathbb{R}\mid x<a\} \]
を無限開区間(infinite open interval)(または非有界開区間(unbounded open interval))という．
特に，$\mathbb{R}=(-\infty ,+\infty )$であり，これらを総称して区間(interval)(または実区間(real interval))という．

$\mathbb{R}$上の区間を一般化した概念は，順序集合の区間にあたる．これについては集合論の記事に譲ることにし，ここでは解析学の立場から$\mathbb{R}$上の区間を考えるものとする．

区間が$\mathbb{R}$の部分集合であることは，定義より明らかである．

記事の公開までもう少しお待ち下さい！
申し訳ございません．現在，こちらの記事は企画中または執筆中または校閲中です．公開までもう少しお待ち下さい．なお，MathAbyssの最新情報はXの公式アカウントまたはLINE公式アカウントにてお知らせしております．また，以下のページにも掲載...
mathabyss.com

区間の例

例1
  • 有界閉区間
  • 半開区間
  • 有界開区間
  • 無限閉区間
  • 無限開区間
図1

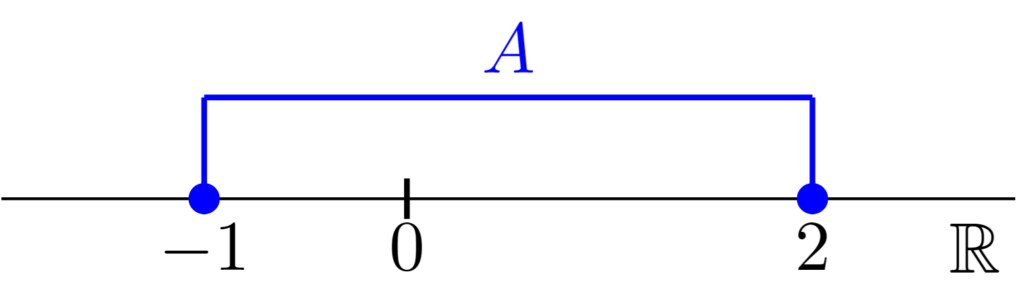
$A=[-1,2]$は有界閉区間であり，図示すると上のようになる．

図2

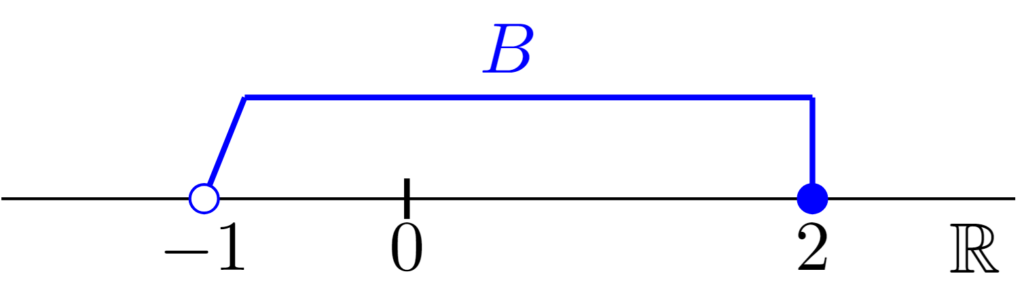
$B=(-1,2]$は半開区間であり，図示すると上のようになる．

図3

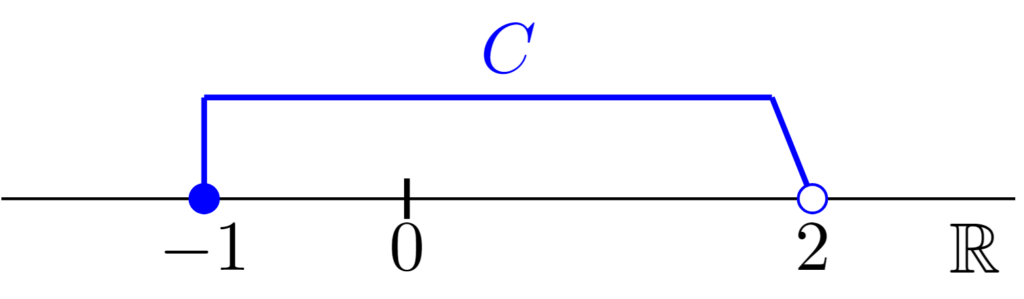
$C=[-1,2)$は半開区間であり，図示すると上のようになる．

図4

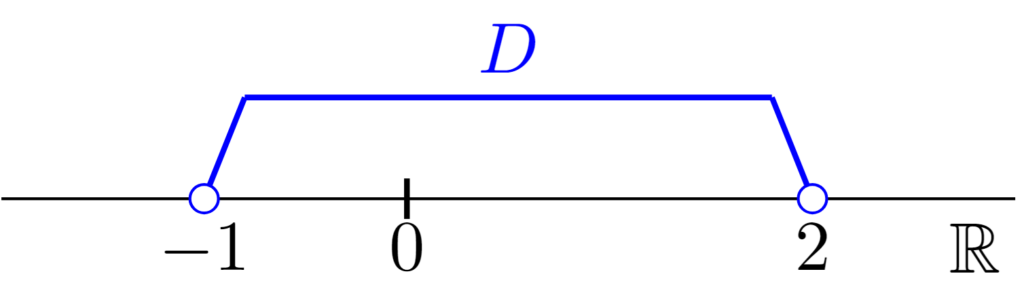
$D=(-1,2)$は有界開区間であり，図示すると上のようになる．

図5

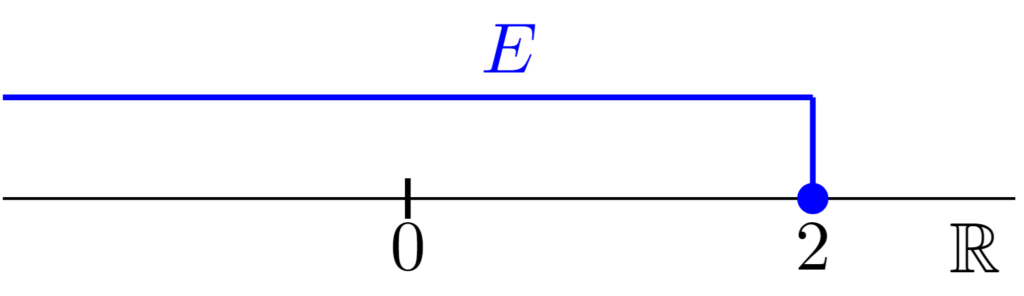
$E=(-\infty ,2]$は無限閉区間であり，図示すると上のようになる．

図6

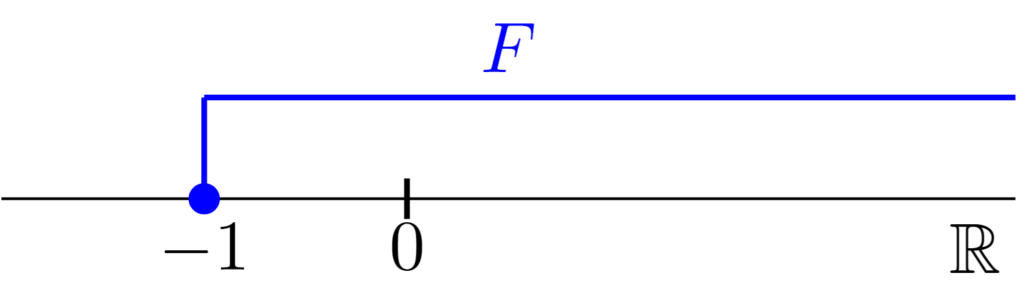
$F=[-1,+\infty )$は無限閉区間であり，図示すると上のようになる．

図7

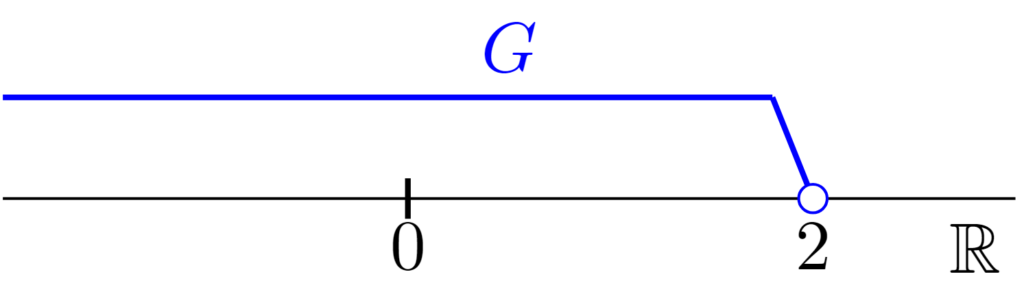
$G=(-\infty ,2)$は無限開区間であり，図示すると上のようになる．

図8

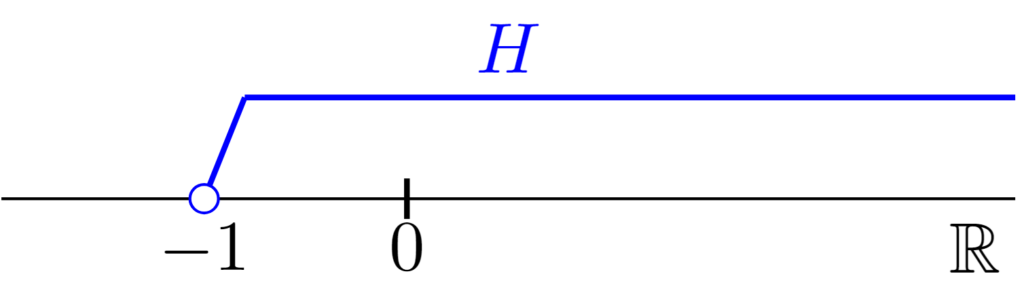
$H=(-1,\infty )$は無限開区間であり，図示すると上のようになる．

区間のイメージ･意義

区間を実数の数直線上に図示すると次のようになる．

図9

区間は，数直線上のひとつながりの部分というイメージで捉えるとよい．そして，閉区間は両端の値を含み，開区間は両端の値を含まない．半開区間は一方の端点の値を含み，もう一方の端点の値を含まない

解析学では，まず微小区間について考えることが多い．例えば，微分では微小区間におけるグラフ上の2点を通る直線の傾きを考え，積分では微小区間における長方形の面積を考える．また，区間の高次元版である微小領域を考えることにより，偏微分や陰関数定理などといった，一般のユークリッド空間での微積分も扱うことができる．その基礎として，実数の区間を考えることには強い意味があるのだ．

関連内容

区間縮小法

区間を考えることにより，実数論における重要な定理を得る．

定理1(区間縮小法(nested intervals))

任意の$n\in \mathbb{N}$に対し，$a_n\le b_n$であるような単調増加数列$\{ a_n\}_{n=1}^{\infty}$，単調減少数列$\{ b_n\}_{n=1}^{\infty}$に対し，有界閉区間の列$\{ I_n\}_{n=1}^{\infty}$を
\[ I_n=[a_n,b_n]\]
により定める．このとき
\[ \bigcap _{n\in \mathbb{N}}I_n\neq \emptyset \]
であり，$\displaystyle \lim_{n\to \infty}(a_n-b_n)=0$ならば，ある$\alpha \in \mathbb{R}$が存在し
\[ \bigcap _{n\in \mathbb{N}}I_n=\{ \alpha \} \]
である．特に
\[ \lim_{n\to \infty}a_n=\lim_{n\to \infty}b_n=\alpha \]
が成り立つ．

区間縮小法とアルキメデスの原理を合わせると，実数の連続性と同値な命題となる．詳細は別記事を参照するとよい．

記事の公開までもう少しお待ち下さい！
申し訳ございません．現在，こちらの記事は企画中または執筆中または校閲中です．公開までもう少しお待ち下さい．なお，MathAbyssの最新情報はXの公式アカウントまたはLINE公式アカウントにてお知らせしております．また，以下のページにも掲載...
mathabyss.com

参考文献

この記事を含め，｢微分積分学｣のカテゴリーに属する記事は，以下の書籍･PDFファイル･Webサイトを参考文献としています(それぞれの記事について，以下に掲載していない参考文献がある場合は，逐一掲載しています)．

書籍

  1. 杉浦光夫, 『解析入門I』, 基礎数学2, 東京大学出版会, 1980年.
  2. 杉浦光夫, 『解析入門II』, 基礎数学3, 東京大学出版会, 1985年.
  3. 杉浦光夫, 清水英男, 金子晃, 岡本和夫, 『解析演習』, 基礎数学7, 東京大学出版会, 1989年.
  4. 高木貞治, 『定本 解析概論』, 岩波書店, 2010年.
  5. 松坂和夫, 『解析入門 上』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  6. 松坂和夫, 『解析入門 中』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  7. 松坂和夫, 『解析入門 下』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  8. 藤岡敦, 『手を動かしてまなぶ ε-δ論法』, 裳華房, 2021年.
  9. 藤岡敦, 『手を動かしてまなぶ 微分積分』, 裳華房, 2019年.
  10. 志賀浩二, 『微分･積分30講』, 数学30講シリーズ1, 朝倉書店, 1988年.
  11. 齋藤正彦, 『齋藤正彦 微分積分学』, 東京図書, 2006年.
  12. 加藤文元, 『大学教養 微分積分』, 数研講座シリーズ, 数研出版, 2019年.
  13. 『大学教養 微分積分』, 加藤文元(監修), 数研出版編集部(編著), チャート式シリーズ, 数研出版, 2019年.
  14. 小寺平治, 『明解演習 微分積分』, 明解演習シリーズ2, 共立出版, 1984年.
補足

10は2024年9月20日に新装改版が発売される予定です．
志賀浩二, 『微分･積分30講』, 数学30講シリーズ1, 新装改版, 朝倉書店, 2024年.

PDFファイル

  1. 石本健太, ｢講義ノート『微分積分学』｣, 2020年, https://www.kurims.kyoto-u.ac.jp/~ishimoto/files/note_calculus.pdf.
  2. 黒田紘敏, ｢微分積分学入門｣, 2024年, https://www7b.biglobe.ne.jp/~h-kuroda/pdf/text_calculus.pdf.
  3. 吉田伸生, ｢微分積分学｣, 2007年, https://ocw.kyoto-u.ac.jp/wp-content/uploads/2021/04/2010_bibunsekibungakuA.pdf.
  4. 西谷達雄, ｢解析学｣, http://www4.math.sci.osaka-u.ac.jp/~nishitani/calculus.pdf.
  5. 松澤寛, ｢解析学の基礎(実数の連続性から定積分の存在まで)｣, https://www.sci.kanagawa-u.ac.jp/math-phys/hmatsu/BasicAnalysis.pdf.
  6. 川端茂徳, ｢解析学入門｣, 2002年, https://www.fit.ac.jp/elec/7_online/calculus.pdf.
  7. 中西敏浩, ｢およそ100ページで学ぶ微分積分学｣, 2021年, https://www.math.shimane-u.ac.jp/~tosihiro/basiccalculus.pdf.

Webサイト

real_intervalこの記事のPDFファイルのダウンロード･印刷はこちらから
タイトルとURLをコピーしました