当サイトの参考文献はこちらからご参照ください．
また，記事中に誤植と思われる箇所を見つけた場合，お手数ですがお問合せフォームからご連絡していただきますと幸いです．

絶対値･三角不等式

微分や積分は極限を用いて定義され，極限は絶対値の不等式を用いて定義される．そのため，極限について考える場合は絶対値とその不等式評価が欠かせない．ここでは，絶対値の定義と，それに付随する重要な不等式である三角不等式について解説する．

絶対値

絶対値を形式的に定義すると，次のようになる．

定義1

$x\in \mathbb{R}$の絶対値(absolute value)$|x|$を次のように定義する．
\[ |x|=\begin{cases}x&(x\ge 0)\\ -x&(x<0)\end{cases}\]

定義1は，次のように言い換えることもできる．

定義2

$x\in \mathbb{R}$の絶対値(absolute value)$|x|$を次のように定義する．
\[ |x|=\max \{ x,-x\} \]

例1
  • $3\ge 0$であるから，$|3|=3$
  • $-\dfrac{1}{2}<0$であるから，$\left| -\dfrac{1}{2}\right| =-\left( -\dfrac{1}{2}\right) =\dfrac{1}{2}$
  • $|x|+|x+1|$について考える．
    $0\le x\le x+1$すなわち$x\ge 0$のとき，$|x|+|x+1|=x+(x+1)=2x+1$
    $x\le 0\le x+1$すなわち$-1\le x\le 0$のとき，$|x|+|x+1|=-x+(x+1)=1$
    $x\le x+1\le 0$すなわち$x\le -1$のとき，$|x|+|x+1|=-x-(x+1)=-2x-1$
    以上より
    \[ |x|+|x+1|=\begin{cases}2x+1&(x\ge 0)\\ 1&(-1\le x\le 0)\\ -2x-1&(x\le -1)\end{cases}\]

絶対値は，視覚的には実数を数直線上の1点として表現したときの，$0$を表す原点からの距離として理解することができる．

絶対値は$0$からのずれを表すことができる．そのため，絶対値を通して$2$と$-2$を同一視することができるようになる．ところが，定義1のように，絶対値は数式を用いると場合分けによって定義されるため，数式処理が面倒であるという難点がある．そこで，人工知能の深層学習などでは差の2乗を計算することによりこれを回避するなどの工夫が行われている．

命題1

$x,y\in \mathbb{R}$に対し，次が成り立つ．

  • (非負性)$|x|\ge 0$
  • (非退化性)$|x|=0\iff x=0$
  • (偶性)$|x|=|-x|$
  • (冪等性)$||x||=|x|$
  • $|x|\ge x$
  • $|x||y|=|xy|$
  • $|x|^2=x^2$
  • $x\ge 0$のとき，$|x|=x\ge 0$
    $x<0$のとき，$|x|=-x>0$
    以上より，示された．$\blacksquare$
  • $|x|=0$ならば，$x\ge 0$と仮定すると$0=|x|=x$より$x=0$であり，$x<0$と仮定すると$0=|x|=-x>0$となり矛盾．よって，$x=0$である．
    逆にこのとき，$|x|=|0|=0$である．$\blacksquare$
  • $x=0$のとき，明らかに$|-x|=|x|$
    $x>0$のとき，$-x<0$であるから$|-x|=x=|x|$
    $x<0$のとき，$-x>0$であるから$|-x|=-x=|x|\blacksquare$
  • ①より$||x||=|(|x|)|=|x|\blacksquare$
  • $x\ge 0$のとき，$|x|=x$
    $x<0$のとき，$|x|=-x>0>x$
    以上より，示された．$\blacksquare$
  • $x\ge 0$かつ$y\ge 0$のとき，$|x||y|=xy\ge 0$より$|xy|=xy=|x||y|$
    $x\ge 0$かつ$y<0$のとき，$|x||y|=x(-y)=-xy\ge 0$すなわち$xy\le 0$より$|xy|=-xy=x(-y)=|x||y|$
    $x<0$かつ$y\ge 0$のとき，$|x||y|=(-x)y=-xy\ge 0$すなわち$xy\le 0$より$|xy|=-xy=(-x)y=|x||y|$
    $x<0$かつ$y<0$のとき，$|x||y|=(-x)(-y)=xy\ge 0$より$|xy|=xy=(-x)(-y)=|x||y|$
    以上より，示された．$\blacksquare$
  • ⑥より$|x|^2=|x||x|=|xx|=|x^2|$
    任意の実数$x$に対し$x^2\ge 0$であるから，$|x^2|=x^2$
    したがって$|x|^2=x^2\blacksquare$

命題1は⑦を場合分けにより示し，それを利用して⑥の両辺を2乗した等式を示すこともできる．

三角不等式

命題1の⑥より，絶対値の積は積の絶対値に等しいが，これは和については当てはまらない．ところが，次のような不等式評価を得ることはできる．

命題2(三角不等式1(triangle inequality))

$x,y\in \mathbb{R}$に対し，次の不等式が成り立つ．
\[ |x+y|\le |x|+|y|\]

\[ \begin{aligned}&(|x|+|y|)^2-|x+y|^2=|x|^2+2|x||y|+|y|^2-(x+y)^2\\ =&x^2+2|xy|+y^2-x^2-2xy-y^2=2(|xy|-xy)\ge 2(xy-xy)=0\end{aligned}\]
以上より$|x+y|^2\le (|x|+|y|)^2$
$|x+y|\ge 0$かつ$|x|+|y|\ge 0$であるから$|x+y|\le |x|+|y|\blacksquare$

三角不等式は，ベクトルや複素数に対しても成り立つ不等式である．

命題3(三角不等式)

$n\in \mathbb{N}$とする．$n$次元ベクトル$\bm{x},\bm{y}$に対し，次の不等式が成り立つ．
\[ \| \bm{x}+\bm{y}\| \le \| \bm{x}\| +\| \bm{y}\| \]

命題4(三角不等式)

$z,w\in \mathbb{C}$に対し，次の不等式が成り立つ．
\[ |z+w|\le |z|+|w|\]

実数は複素数の一種であり，複素数は複素平面上ではベクトルと同様に扱うことができる．三角不等式はベクトルを用いると以下の図のように可視化することができる．

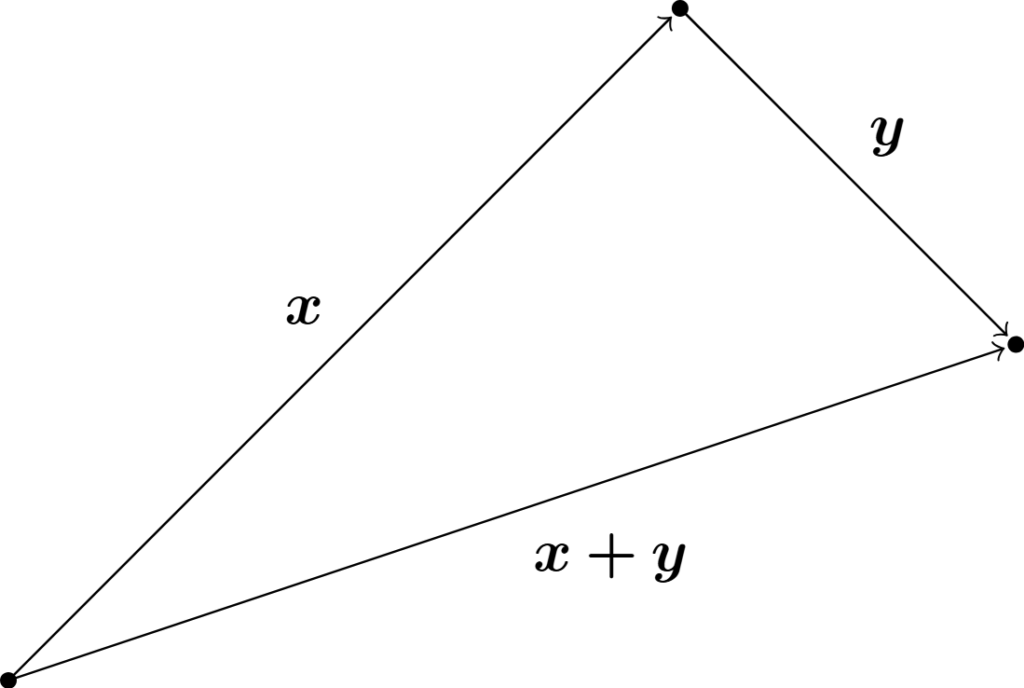
上の図では，三角形の2辺の長さの和が，残り1辺の長さよりも長いことから，明らかに
\[ \| \bm{x}+\bm{y}\| \le \| \bm{x}\| +\| \bm{y}\| \]
が成り立つことが分かる．

三角不等式の派生

命題5

$n\in \mathbb{N},x_1,x_2,\dots ,x_n,x,y,z\in \mathbb{R}$に対し，次が成り立つ．

  • $\displaystyle \left| \sum_{i=1}^nx_i\right| \le \sum_{i=1}^n|x_i|$
  • $|x-z|\le |x-y|+|y-z|$
  • $|x|-|y|\le |x-y|$
  • $||x|-|y||\le |x-y|$
  • $||x|-|y||\le |x+y|$
  • $n$に関する数学的帰納法で示す．
    $n=1$のとき
    \[ \left| \sum_{i=1}^1x_i\right| =|x_1|=\sum_{i=1}^1|x_i|\]
    より明らかに成り立つ．
    $n=k$で与式が成り立つと仮定すると，三角不等式より
    \[ \left| \sum_{i=1}^{k+1}x_i\right| =\left| \sum_{i=1}^kx_i+x_{k+1}\right| \le \left| \sum_{i=1}^kx_i\right| +|x_{k+1}| \le \sum_{i=1}^k|x_i|+|x_{k+1}|=\sum_{i=1}^{k+1}|x_i|\]
    であるから，$n=k+1$のときも成り立つ．
    以上より，任意の$n\in \mathbb{N}$に対し，与式が成り立つ．$\blacksquare$
  • 三角不等式より
    \[ |x-z|=|(x-y)-(y-z)|\le |x-y|+|y-z|\]
    したがって，示された．$\blacksquare$
  • 三角不等式より
    \[ |x|-|y|=|(x-y)+y|-|y|\le |x-y|+|y|-|y|=|x-y|\]
    したがって，示された．$\blacksquare$
  • 三角不等式より
    \[ \begin{aligned}||x|-|y||&=||(x-y)+y|-|y||\le ||x-y|+|y|-|y||\\ &=||x-y||=|x-y|\end{aligned}\]
    したがって，示された．$\blacksquare$
  • ③より
    \[ \begin{aligned}||x|-|y||&=||x|-|-y||=||x|-|x-(x+y)||\\ &\le ||x|-(|x|-|x+y|)|=||x+y||=|x+y|\end{aligned}\]
    したがって，示された．$\blacksquare$

命題5は三角不等式の証明と同様に，両辺を2乗した不等式を示すこともできる．

参考文献

この記事を含め，｢微分積分学｣のカテゴリーに属する記事は，以下の書籍･PDFファイル･Webサイトを参考文献としています(それぞれの記事について，以下に掲載していない参考文献がある場合は，逐一掲載しています)．

書籍

  1. 杉浦光夫, 『解析入門I』, 基礎数学2, 東京大学出版会, 1980年.
  2. 杉浦光夫, 『解析入門II』, 基礎数学3, 東京大学出版会, 1985年.
  3. 杉浦光夫, 清水英男, 金子晃, 岡本和夫, 『解析演習』, 基礎数学7, 東京大学出版会, 1989年.
  4. 高木貞治, 『定本 解析概論』, 岩波書店, 2010年.
  5. 松坂和夫, 『解析入門 上』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  6. 松坂和夫, 『解析入門 中』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  7. 松坂和夫, 『解析入門 下』, 松坂和夫 数学入門シリーズ, 新装版, 岩波書店, 2018年.
  8. 藤岡敦, 『手を動かしてまなぶ ε-δ論法』, 裳華房, 2021年.
  9. 藤岡敦, 『手を動かしてまなぶ 微分積分』, 裳華房, 2019年.
  10. 志賀浩二, 『微分･積分30講』, 数学30講シリーズ1, 新装改版, 朝倉書店, 2024年.
  11. 齋藤正彦, 『齋藤正彦 微分積分学』, 東京図書, 2006年.
  12. 加藤文元, 『大学教養 微分積分』, 数研講座シリーズ, 数研出版, 2019年.
  13. 『大学教養 微分積分』, 加藤文元(監修), 数研出版編集部(編著), チャート式シリーズ, 数研出版, 2019年.
  14. 小寺平治, 『明解演習 微分積分』, 明解演習シリーズ2, 共立出版, 1984年.

PDFファイル

  1. 石本健太, ｢講義ノート『微分積分学』｣, 2020年, https://www.kurims.kyoto-u.ac.jp/~ishimoto/files/note_calculus.pdf.
  2. 黒田紘敏, ｢微分積分学入門｣, 2024年, https://www7b.biglobe.ne.jp/~h-kuroda/pdf/text_calculus.pdf.
  3. 吉田伸生, ｢微分積分学｣, 2007年, https://ocw.kyoto-u.ac.jp/wp-content/uploads/2021/04/2010_bibunsekibungakuA.pdf.
  4. 西谷達雄, ｢解析学｣, http://www4.math.sci.osaka-u.ac.jp/~nishitani/calculus.pdf.
  5. 松澤寛, ｢解析学の基礎(実数の連続性から定積分の存在まで)｣, https://www.sci.kanagawa-u.ac.jp/math-phys/hmatsu/BasicAnalysis.pdf.
  6. 川端茂徳, ｢解析学入門｣, 2002年, https://www.fit.ac.jp/elec/7_online/calculus.pdf.
  7. 中西敏浩, ｢およそ100ページで学ぶ微分積分学｣, 2021年, https://www.math.shimane-u.ac.jp/~tosihiro/basiccalculus.pdf.

Webサイト

  1. 三角関数を含んだ不等式のことを｢三角不等式(trigonometric inequalities)｣と呼ぶこともあるが，一般には(特に大学数学においては)｢三角不等式｣という語は絶対値についての不等式の意味で用いられることが多いため，注意が必要である．ちなみに，当サイトではtrigonometric inequalitiesを｢三角関数を含む不等式｣と呼ぶことで日本語でも明確に区別するようにしている． ↩︎
タイトルとURLをコピーしました