部分集合とは,簡単に言えば「集合の一部分からなる集合」のことであり,冪集合は部分集合全体の集合である.
部分集合
集合$A,B$について,$A$の任意の元が$B$の元であるとき,$A$を$B$の部分集合(subset)といい,$B$を$A$の上位集合(superset)という.また,このとき$A$は$B$に含まれる(または包含される,包まれる,包摂される,内包される)または$B$は$A$を含む(または包含する,包む,包摂する,内包する)といい,$A\subset B$(または$B\supset A$)で表す.
特に,空集合$\emptyset$は任意の集合の部分集合であると考える.
$A\subset B$かつ$A\neq B$のとき,$A$は$B$の真部分集合(proper subset)(または狭義部分集合(strict subset))であるといい,$A\subsetneq B$(または$B\supsetneq A$)で表す.
- ある集合$X$を考える.任意の$x\in X$に対し,明らかに$x\in X$であるから,$X\subset X$である.特に,$X=X$であるから$X$は$X$の真部分集合でない.
- 任意の$n\in \mathbb{N}$に対し,$n\in \mathbb{Z}$であるから(任意の正の整数は整数であるから),$\mathbb{N}\subset \mathbb{Z}$である.特に,$\mathbb{N}\neq \mathbb{Z}$であるから$\mathbb{N}\subsetneq \mathbb{Z}$である.
$A\subset B$を$A\subseteq B$で表し,$A\subsetneq B$を$A\subset B$で表す流儀もある.
ここでは素朴集合論における部分集合の定義を述べたが,公理的集合論における部分集合の定義も重要である.
集合$x,y$に対して,$x\subset y$を次のように定める.
\[ x\subset y\stackrel{\mathrm{def}}{\iff}\forall a[a\in x\implies a\in y]\]
例2を定義3に従って再考してみる.
- $\forall x[x\in X\implies x\in X]$は真であるから,$X\subset X$である.
- $\forall n[n\in \mathbb{N}\implies n\in \mathbb{Z}]$は真であるから,$\mathbb{N}\subset \mathbb{Z}$である.
複数の集合が与えられたとき,部分集合であるという関係は包含関係(inclusion, containment)と呼ばれる.包含関係を証明するときは,公理的集合論の部分集合の定義に従って論証することが多い.
部分集合のイメージと意義
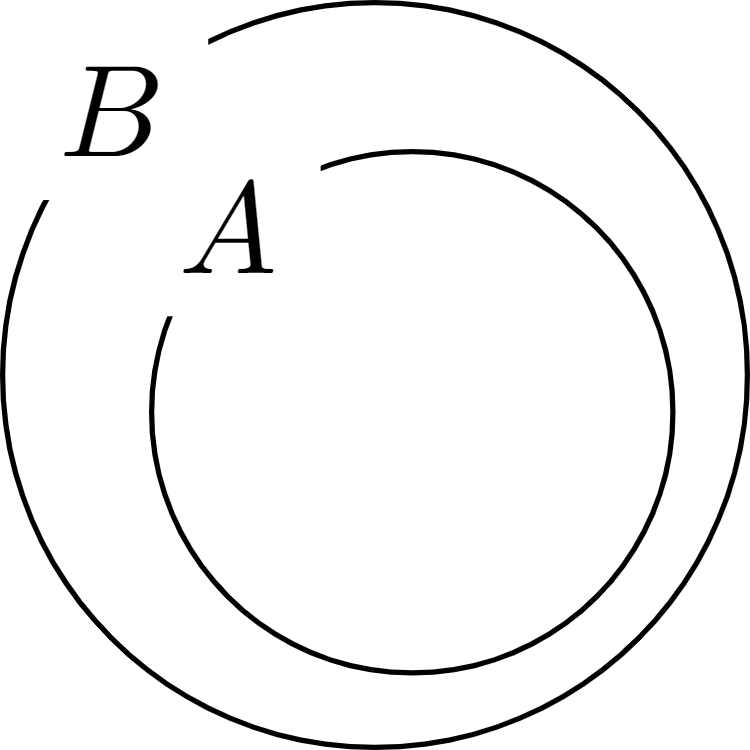
集合$A,B$に対し,$A\subset B$という包含関係をオイラー図によって表すと図1のようになる.図1を見ると,$A\subset B$を「$A$は$B$に含まれる」といった表現をする理由が直感的に理解できる.
集合の包含関係は,実数の大小関係と対応させて考えると,より深い理解に繋がる.実数の大小関係を厳密に定義するためには,有理数の集合を切断したり完備化したりすることによって実数を構成するところから始める必要がある.そのため,ここでは実数の大小関係は直感的に次のように「定義」することにする1.
$a,b\in \mathbb{R}$に対し,$a$が$b$より小さい(または$b$は$a$より大きい)とき,$a<b$(または$b>a$)で表す.
$a<b$かつ$a=b$であるとき,$a$は$b$以下である(または$b$は$a$以上である)といい,$a\le b$(または$b\ge a$)で表す.
これを集合の包含関係と対応させると,次のようになる.
| 集合の大小関係 | 実数の大小関係 | ||
| $A\subsetneq B$ | $A=B$ | $a<b$ | $a=b$ |
| $A\subset B$ | $a\le b$ | ||
このように考えると,部分集合の記号を$\subset$と$\subseteq$を用いて表す流儀は,$<$と$\le$と対応させると,ごく自然なことであると言える.
つまり,集合の包含関係は,集合のある種の「大小関係」である.実数で大小関係を考えることの重要性と同様に,集合で包含関係を考えることもまた,集合の世界にある種の「順序」を取り入れるという点で非常に重要である.
集合の相等関係
素朴集合論では,2つの集合が等しいことを次のように定義する.
集合$A,B$について,$A$と$B$の元が一致するとき,$A$と$B$は等しいといい,$A=B$で表す.
次の集合$X,Y$について考える.
\[ X=\{ x\in \mathbb{R}\mid x^2-3x+2=0\} ,Y=\{ 1,2\} \]
$x^2-3x+2=0$なる$x\in \mathbb{R}$は$x=1,2$であるから,$X=\{ 1,2\} =Y$
公理的集合論では,外延性公理(axiom of extensionality)によって,集合の相等関係を次のように認めている.
\[ \forall x\forall y[\forall z[z\in x\iff z\in y]\implies x=y]\]
この公理は,集合が元によって一意に定まるものであることを主張している.例えば,$\{ a,b\}$という集合と$\{ b,a\} ,\{ a,a,b\}$といった集合は区別せず,すべて同じ集合を表していると考える.
また,等号は次のような公理を満たすものとして定義されている.
- [反射律(law of identity)]
\[ \forall x[x=x]\] - [代入原理(substitution property)]
\[ \forall x\forall y[x=y\implies \forall \phi [\phi (x)\implies \phi (y)]\]
公理2を用いることで,外延性公理の逆命題が成り立つことが分かる.
\[ \forall x\forall y[\forall z[z\in x\iff z\in y]\iff x=y]\]
外延性公理より,次の命題を示せば十分である.
\[ \forall x\forall y[x=y\implies \forall z[z\in x\iff z\in y]]\]
集合$t$に関する命題$\phi (t)$を$z\in t$により定める.
等号の代入原理より,$x=y$ならば($\phi (x)$ならば$\phi (y)$),すなわち($z\in x$ならば$z\in y$)が成り立つ.
ここで,集合$t$に関する命題$\psi (t)$を$t=x$により定めると,等号の反射律より$x=x$であるから$\phi (x)$である.よって,等号の代入原理より,$x=y$ならば$\phi (y)$,すなわち$y=x$である.
$y=x$より,同様に考えると,($z\in y$ならば$z\in x$)が成り立つ.
以上より,$x=y$ならば,($z\in x$ならば$z\in y$)かつ($z\in y$ならば$z\in x$)が成り立つ.したがって,$z\in x$であることと$z\in y$であることは同値であるから,示された.$\blacksquare$
また,定義2と公理1及び公理2を合わせて考えると,次の同値関係が成り立つことが分かる.
集合$A,B$に対して,$A=B$であることと,$A\subset B$かつ$B\subset A$であることは同値である.
定義2より,$A=B$ならば$A\subset B$であり,$B\subset A$である.
逆にこのとき,$A\subset B$より任意の$x\in A$は$x\in B$であり,$B\subset A$より任意の$x\in B$は$x\in A$であるから,任意の$x$に対し,$x\in A$であることと$x\in B$であることは同値である.よって,$A=B$である.$\blacksquare$
集合の相等関係を証明するときは,命題2を用いて,集合の包含関係の証明に帰着させて論証することが多い.
重要な包含関係
次の包含関係が成り立つことは明らかである.
\[ \emptyset \subsetneq \mathbb{N}\subsetneq \mathbb{Z}\subsetneq \mathbb{Q}\subsetneq \mathbb{R}\subsetneq \mathbb{C}\]
当たり前のように思えるかもしれないが,これは数の集合を明確に定義するときに重要である.例えば,正の整数全体の集合$\mathbb{N}$は,ペアノの公理を満たすものとして定義される.そして,加法や乗法といった演算を導入し,加法の逆元を導入して整数全体の集合$\mathbb{Z}$に拡張する.さらに,乗法の逆元を導入して有理数全体の集合$\mathbb{Q}$に拡張したあと,切断や完備化を行うことにより実数全体の集合$\mathbb{R}$が得られる.ここに虚数単位$i$を添加すると複素数全体の集合$\mathbb{C}$を構成できる.
このように,数の集合を明確に定義し,構成するには,包含関係において最も「小さい」集合から始めて,集合を「大きく」していくという過程をとることになるのである.
包含関係の性質
最後に,包含関係の重要な性質を紹介する.
まず,ここまでで既に紹介した性質をまとめておこう.
- 任意の集合$A$に対し,$\emptyset \subset A$
- (反射律(reflexive law))任意の集合$A$に対し,$A\subset A$
- 集合$A,B$に対し,$A=B$であることと,$A\subset B$かつ$B\subset A$であることは同値である.
そして,もう1つ重要な性質がある.
集合$A,B,C$に対し,($A\subset B$かつ$B\subset C$)ならば$A\subset C$
$x\in A$ならば,$A\subset B$より$x\in B$である.また,このとき$B\subset C$より$x\in C$である.よって,$A\subset C$である.$\blacksquare$
冪集合
元が集合であるような集合,すなわち「集合の集合」も考えることができる.
$A$を集合とする.$A$の部分集合全体の集合を$A$の冪集合(power set)(または部分集合族(family of subsets))といい,$2^A$(または$\mathfrak{P}(S),\mathcal{P}(S),\mathfrak{pow}(S),\mathrm{Power}(S),\Pi (S),\mathbb{P}(S),\wp (S)$)で表す.
冪集合の表記に注目すると,$2$の指数に集合$A$があるように捉えることができる.このように表記するのは,次の命題が成り立つからである.
$A$を集合とするとき,次の等式が成り立つ.
\[ \sharp 2^A=2^{\sharp A}\]
$\sharp A=n\in \mathbb{N}$とおく.互いに異なる$a_1,a_2,\dots ,a_n$を用いて$A=\{ a_1,a_2,\dots ,a_n\}$と表されるとき,$A$の任意の部分集合$B$を構成する元は,$1$以上$n$以下の任意の整数$i$に対して,$a_i\in B$または$a\not\in B$のいずれか一方が成り立つ.よって,$A$の部分集合の個数は$2^n$個であるから,与式が成り立つ.$\blacksquare$
公理的集合論では,冪集合公理(axiom of power set)によって,冪集合の存在が保証されている.
\[ \forall x\exists y\forall z[z\in y\iff \forall w[w\in z\implies w\in x]]\]
冪集合は,集合を元に持つ集合であり,このようなものは集合族3と呼ばれる.集合族については別記事で詳しく取り上げているので,参照してほしい.
- 実数の大小関係の厳密な定義は以下を参照するとよい.
原隆, 「実数の構成に関するノート」, 2018年, https://www2.math.kyushu-u.ac.jp/~hara/lectures/08/realnumbersv2.pdf. ↩︎ - この命題を厳密に証明するには,数の集合の構成を考える必要がある.参考文献の書籍の2を参照するとよい.
齋藤正彦, 『数学の基礎: 集合・数・位相』, 基礎数学14, 東京大学出版会, 2002年. ↩︎ - 別記事で扱った集合族の厳密な定義を参照せよ. ↩︎

