1次独立・1次従属
$\mathbb{R}^3$において,2つのベクトル$\bm{a},\bm{b}\in \mathbb{R}^3$が与えられたとき,例えば次のような平面$\alpha$が定まる.
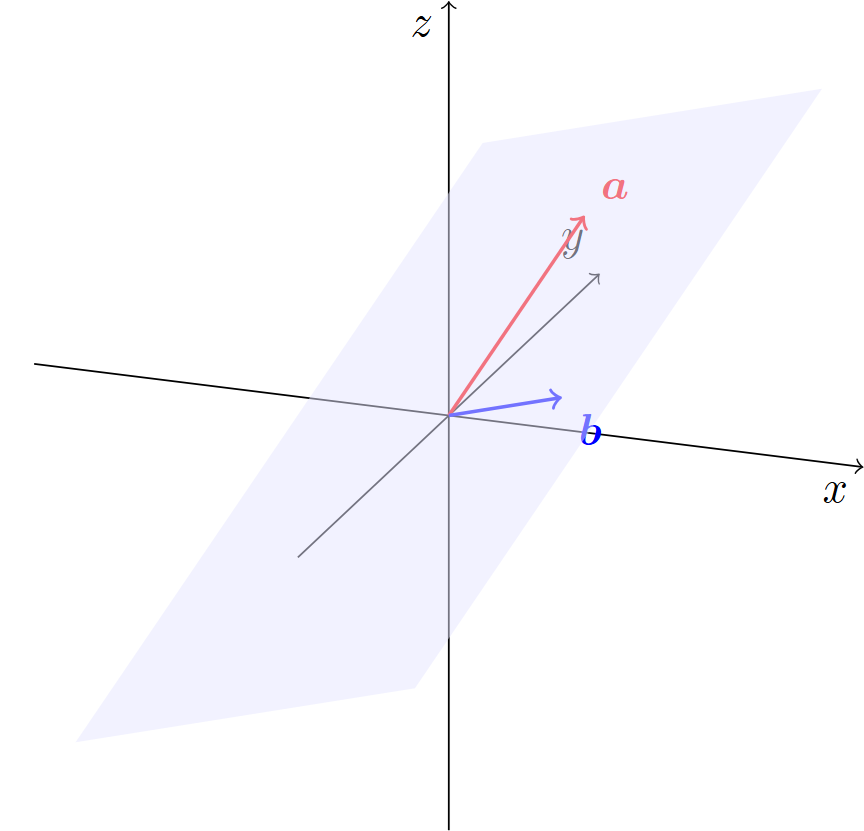
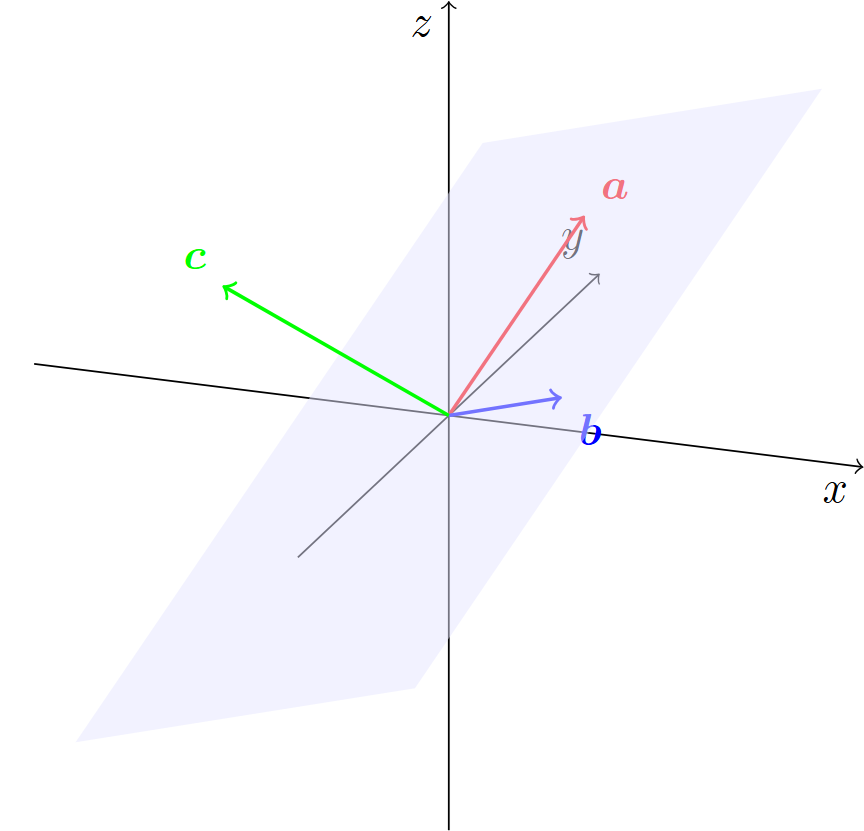
このとき,もう1つのベクトル$\bm{c}\in \mathbb{R}^3$を考えるとき,$\bm{c}$の選び方によっては,次の図のように,$\bm{c}$が平面$\alpha$を飛び出す場合がある.
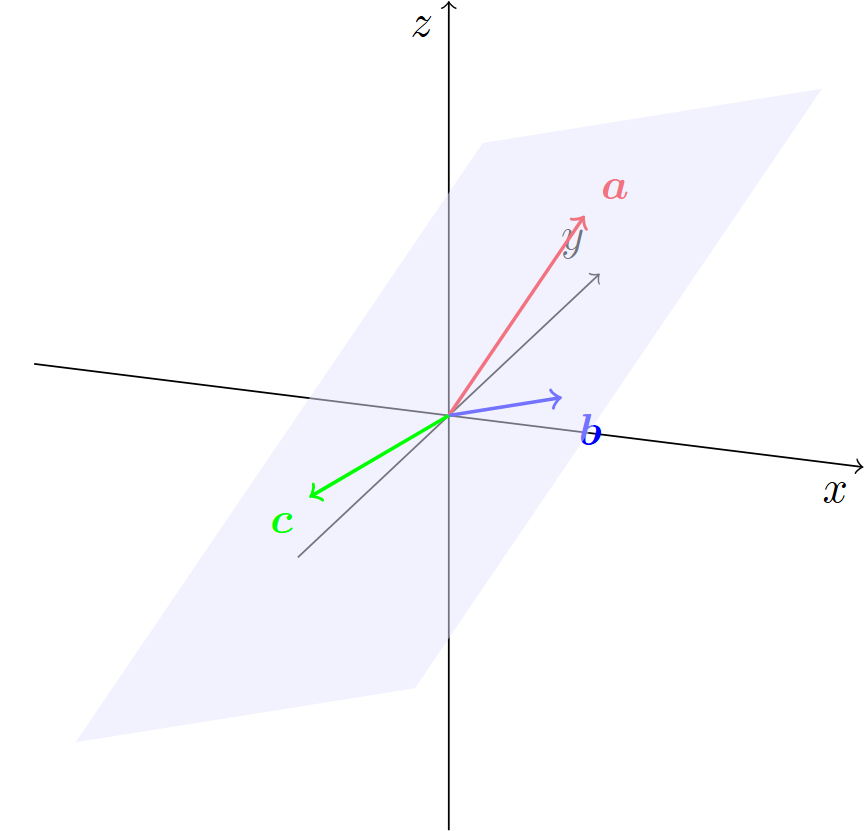
また,次の図のように,$\bm{c}$が平面$\alpha$上に存在する場合もある.
前者の場合,$\bm{c}$は平面$\alpha$にはない新たな向きを定めるベクトルであると考えることができ,$\bm{a},\bm{b},\bm{c}$は「向き」について,互いに「独立」していると捉えることができる.
一方で,後者の場合,$\bm{c}$は平面$\alpha$に既に備え付けられていた向きのベクトルであると考えることができ,$\bm{a},\bm{b},\bm{c}$は「向き」について,互いに「独立」しているとは言えそうにない.
このように,ベクトルの向きのばらつきを評価する概念として,1次独立と1次従属を定義する.
$n\in \mathbb{N}$,$K$を体1,$V$を$K$上のベクトル空間,$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n\in V$,$k_1,k_2,\dots ,k_n\in K$とする.
- $k_1\bm{x}_1+k_2\bm{x}_2+\dots +k_n\bm{x}_n$を$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$の$1$次結合(または線形結合(linear combination),線形和)(superposition)という.
- 等式
\[ k_1\bm{x}_1+k_2\bm{x}_2+\dots +k_n\bm{x}_n=\bm{0}\tag{$\ast$}\]
を$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$の$1$次関係(または線形関係)という. - $(\ast )$が成り立つことと
\[ k_1=k_2=\dots =k_n=0\]
であることが同値であるとき,$(\ast )$を$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$の自明な$1$次関係といい,$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$は互いに$1$次独立(または線形独立(linearly independent))であるという. - $\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$が$1$次独立でないとき,$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$は$1$次従属(または線形従属(linearly dependent))であるという.
1次独立・1次従属の例
具体的なベクトルについて,1次独立と1次従属を確認しよう.
$\mathbb{R}$上のベクトル空間$\mathbb{R}^3$において
\[ \bm{x}=\begin{pmatrix}2\\ -1\\ 3\end{pmatrix},\quad \bm{y}=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix},\quad \bm{z}=\begin{pmatrix}0\\ 1\\ 1\end{pmatrix}\]
は互いに$1$次独立である.
実際,$k_1,k_2,k_3\in \mathbb{R}$が
\[ k_1\bm{x}+k_2\bm{y}+k_3\bm{z}=\bm{0}\]
を満たすならば
\[ k_1\begin{pmatrix}2\\ -1\\ 3\end{pmatrix}+k_2\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}+k_3\begin{pmatrix}0\\ 1\\ 1\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}\]
すなわち
\[ \begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&1\end{pmatrix}\begin{pmatrix}k_1\\ k_2\\ k_3\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}\]
であるから,これが自明な解しか持たない,すなわち
\[ A=\begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&1\end{pmatrix}\]
の階数が$3$であることを確かめればよい2.$A$を簡約化すると
\[ \begin{aligned}&\begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&1\end{pmatrix}\\ \xrightarrow{\tiny 第1行と第2行を交換}&\begin{pmatrix}-1&1&1\\ 2&1&0\\ 3&0&1\end{pmatrix}\\ \xrightarrow{\tiny 第2行に第1行\times 2を足し,第3行に第1行\times 3を足す}&\begin{pmatrix}-1&1&1\\ 0&3&2\\ 0&3&4\end{pmatrix}\\ \xrightarrow{\tiny 第1行\times (-1)}&\begin{pmatrix}1&-1&-1\\ 0&3&2\\ 0&3&4\end{pmatrix}\\ \xrightarrow{\tiny 第3行に第2行\times (-1)を足す}&\begin{pmatrix}1&-1&-1\\ 0&3&2\\ 0&0&2\end{pmatrix}\\ \xrightarrow{\tiny 第2行に第3行\times (-2)を足す}&\begin{pmatrix}1&-1&-1\\ 0&3&0\\ 0&0&2\end{pmatrix}\\ \xrightarrow{\tiny 第2行\times \frac{1}{3},第3行\times \frac{1}{2}}&\begin{pmatrix}1&-1&-1\\ 0&1&0\\ 0&0&1\end{pmatrix}\\ \xrightarrow{\tiny 第1行に第2行と第3行を足す}&\begin{pmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}\end{aligned}\]
となるから
\[ \operatorname{rank}A=3\]
である.
$\mathbb{R}$上のベクトル空間$\mathbb{R}^3$において
\[ \bm{x}=\begin{pmatrix}2\\ -1\\ 3\end{pmatrix},\quad \bm{y}=\begin{pmatrix}1\\ 1\\ 0\end{pmatrix},\quad \bm{z}=\begin{pmatrix}0\\ 1\\ -1\end{pmatrix}\]
は$1$次従属である.
実際,$k_1,k_2,k_3\in \mathbb{R}$が
\[ k_1\bm{x}+k_2\bm{y}+k_3\bm{z}=\bm{0}\]
を満たすならば
\[ k_1\begin{pmatrix}2\\ -1\\ 3\end{pmatrix}+k_2\begin{pmatrix}1\\ 1\\ 0\end{pmatrix}+k_3\begin{pmatrix}0\\ 1\\ -1\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}\]
すなわち
\[ \begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&-1\end{pmatrix}\begin{pmatrix}k_1\\ k_2\\ k_3\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}\]
であるから,これが非自明な解を持つ,すなわち
\[ A=\begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&-1\end{pmatrix}\]
の階数が$3$でないことを確かめればよい.$A$を簡約化すると
\[ \begin{aligned}&\begin{pmatrix}2&1&0\\ -1&1&1\\ 3&0&-1\end{pmatrix}\\ \xrightarrow{\tiny 第1行と第2行を交換}&\begin{pmatrix}-1&1&1\\ 2&1&0\\ 3&0&-1\end{pmatrix}\\ \xrightarrow{\tiny 第2行に第1行\times 2を足し,第3行に第1行\times 3を足す}&\begin{pmatrix}-1&1&1\\ 0&3&2\\ 0&3&2\end{pmatrix}\\ \xrightarrow{\tiny 第1行\times (-1)}&\begin{pmatrix}1&-1&-1\\ 0&3&2\\ 0&3&2\end{pmatrix}\\ \xrightarrow{\tiny 第3行に第2行\times (-1)を足す}&\begin{pmatrix}1&-1&-1\\ 0&3&2\\ 0&0&0\end{pmatrix}\\ \xrightarrow{\tiny 第2行\times \frac{1}{3}}&\begin{pmatrix}1&-1&-1\\ 0&1&\frac{2}{3}\\ 0&0&0\end{pmatrix}\\ \xrightarrow{\tiny 第1行に第2行を足す}&\begin{pmatrix}1&0&-\frac{1}{3}\\ 0&1&\frac{2}{3}\\ 0&0&0\end{pmatrix}\end{aligned}\]
となるから
\[ \operatorname{rank}A=2\]
である.
具体的には,$\bm{x},\bm{y},\bm{z}$は
\[ \bm{x}-2\bm{y}+3\bm{z}=\bm{0}\]
という自明でない$1$次関係を持つ.
例1や例2のように,$\mathbb{R}^n$の$n$本のベクトルが$1$次独立であるかどうかを調べる場合は,次のように確かめることができる.
$n\in \mathbb{N}$,$K$を体,$\mathbb{R}^n$を$K$上のベクトル空間,$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n\in \mathbb{R}^n$とする.
$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$が$1$次独立であるための必要十分条件は
\[ \begin{vmatrix}\bm{x}_1&\bm{x}_2&\cdots &\bm{x}_n\end{vmatrix}\neq 0\]
$\bm{x}_1,\bm{x}_2,\dots ,\bm{x}_n$が$1$次独立,すなわち$k_1,k_2,\dots ,k_n\in K$が
\[ k_1\bm{x}_1+k_2\bm{x}_2+\dots +k_n\bm{x}_n=\bm{0}\]
を満たすことと
\[ k_1=k_2=\dots =k_n=0\]
が同値であることは,$k_1,k_2,\dots ,k_n\in K$についての連立$1$次方程式
\[ \begin{pmatrix}\bm{x}_1&\bm{x}_2&\cdots &\bm{x}_n\end{pmatrix}\begin{pmatrix}k_1\\ k_2\\ \vdots \\ k_n\end{pmatrix}=\bm{0}\]
が自明な解のみを持つことと同値である.
\[ \begin{pmatrix}\bm{x}_1&\bm{x}_2&\cdots &\bm{x}_n\end{pmatrix}\]
が$n$次正方行列であることに注意すると,これは,係数行列が正則であること,すなわち
\[ \begin{vmatrix}\bm{x}_1&\bm{x}_2&\cdots &\bm{x}_n\end{vmatrix}=0\]
であることと同値である.$\blacksquare$
特に,次のベクトルの組は重要である.
$n\in \mathbb{N}$,$i\in \{ 1,2,\dots ,n\}$とする.
$\mathbb{R}^n$のベクトルのうち,第$i$成分が$1$で,それ以外の任意の成分が$0$であるものを$\mathbb{R}^n$の単位ベクトル(または基本ベクトル)(unit vector)といい,$\bm{e}_i$で表す.すなわち
\[ \bm{e}_1=\begin{pmatrix}1\\ 0\\ \vdots \\ 0\end{pmatrix},\quad \bm{e}_2=\begin{pmatrix}0\\ 1\\ \vdots \\ 0\end{pmatrix},\quad \dots ,\quad \bm{e}_n=\begin{pmatrix}0\\ 0\\ \vdots \\ 1\end{pmatrix}\]
このベクトルが重要であることの理由の1つとして,次の性質がある.
$n\in \mathbb{N}$,$K$を体とする.
$K$上のベクトル空間$\mathbb{R}^n$において,$\mathbb{R}^n$の単位ベクトル$\bm{e}_1,\bm{e}_2,\dots ,\bm{e}_n$は互いに$1$次独立である.
$k_1,k_2,\dots ,k_n\in K$が
\[ k_1\bm{e}_1+k_2\bm{e}_2+\dots +k_n\bm{e}_n=\bm{0}\]
を満たすならば
\[ k_1\begin{pmatrix}1\\ 0\\ \vdots \\ 0\end{pmatrix}+k_2\begin{pmatrix}0\\ 1\\ \vdots \\ 0\end{pmatrix}+\dots +k_n\begin{pmatrix}0\\ 0\\ \vdots \\ 1\end{pmatrix}=\begin{pmatrix}0\\ 0\\ \vdots \\ 0\end{pmatrix}\]
すなわち
\[ \begin{pmatrix}k_1\\ k_2\\ \vdots \\ k_n\end{pmatrix}=\begin{pmatrix}0\\ 0\\ \vdots \\ 0\end{pmatrix}\]
であるから
\[ k_1=k_2=\dots =k_n=0\]
を得る.したがって,$\bm{e}_1,\bm{e}_2,\dots ,\bm{e}_n$は互いに$1$次独立である.$\blacksquare$
また,あまり考えることは少ないが,1つのベクトルが$1$次独立性は次のようにまとめられる.
$K$を体,$V$を$K$上のベクトル空間.$\bm{x}\in V$とする.
- $\bm{x}$が$1$次独立であるための必要十分条件は$\bm{x}\neq \bm{0}$である.
- $\bm{x}$が$1$次従属であるための必要十分条件は$\bm{x}=\bm{0}$である.
①の対偶は②であるから,②を示す.
まず,必要性を示す.
$\bm{x}$が$1$次従属ならば,ある$k\in K\setminus \{ \bm{0}\}$が存在して,$k\bm{x}=\bm{0}$となる.よって
\[ \bm{x}=1\bm{x}=(k^{-1}k)\bm{x}=k^{-1}(k\bm{x})=k^{-1}\bm{0}=\bm{0}\]
次に,十分性を示す.
$\bm{x}=\bm{0}$ならば,任意の$k\in K$に対して,$k\bm{x}=\bm{0}$が成り立つ.
よって,$\bm{x}$は$1$次従属である.$\blacksquare$

