上界･下界～定義･イメージ･例を解説～

upper_bound-lower_bound-calculus この記事のPDFファイルのダウンロード･印刷はこちらから

上界とは，実数の部分集合のどの元よりも大きい実数のことです．
下界とは，実数の部分集合のどの元よりも小さい実数のことです．

上界･下界とは

$A$を$\mathbb{R}$の空でない部分集合とする．ある$M\in \mathbb{R}$が存在し，任意の$x\in A$に対し，$x\le M$となるとき，$M$を$A$の上界(upper bound)という．また，ある$m\in \mathbb{R}$が存在し，任意の$x\in A$に対し，$m\le x$となるとき，$m$を$A$の下界(lower bound)という．

上界･下界の定義
上界･下界のイメージ･例･意義
関連内容
1. 上界･下界と最大値･最小値
2. 上界･下界に似た概念
参考文献

上界･下界の定義

上界･下界の厳密な定義は次のようになります．

定義1

$A$を$\mathbb{R}$の空でない部分集合とする．ある$a\in \mathbb{R}$が存在し，任意の$x\in A$に対し，$x\le a$となるとき，$a$を$A$の上界(upper bound)という．また，ある$b\in \mathbb{R}$が存在し，任意の$x\in A$に対し，$b\le x$となるとき，$b$を$A$の下界(lower bound)という．

$A$に上界が存在するとき，$A$は上に有界(bounded above)であるといい，下界が存在するとき，$A$は下に有界(bounded below)であるという．$A$が上に有界かつ下に有界であるとき，$A$は有界(bounded)であるという．

$\mathbb{R}$上の上界･下界を一般化した概念は，順序集合の上界･下界にあたる．これについては集合論の記事に譲ることにし，ここでは解析学の立場から$\mathbb{R}$上の上界･下界を考えるものとする．

記事の公開までもう少しお待ち下さい！

申し訳ございません．現在，こちらの記事は企画中または執筆中または校閲中です．公開までもう少しお待ち下さい．なお，MathAbyssの最新情報はXの公式アカウントまたはLINE公式アカウントにてお知らせしております．また，以下のページにも掲載...

さて，上の定義を論理式を用いて表してみよう．空でない$A\subset \mathbb{R}$に対し，$A$の上界$a$と下界$b$は，それぞれ次の条件を満たす．

\[ \forall x\in A[x\le a]\]
\[ \forall x\in A[b\le x]\]

ここで，当たり前かもしれないが，$x\le a$や$b\le x$といった不等式について，等号が成り立つのは，それぞれ$x$が$A$の上界，下界と一致するときである．

そして，$A$に最大値や最小値が存在するとき，その値はそれぞれ$A$の上界･下界でもある．定義を見れば明らかだが，最大値･最小値は上界･下界の1つに過ぎない．

最大値･最小値～定義･イメージ･例を解説～

maximum-minimumこの記事のPDFファイルのダウンロード･印刷はこちらから最大値とは，実数の部分集合の元の中で，最も大きい元のことです．最小値とは，実数の部分集合の元の中で，最も小さい元のことです．最大値･最小値とは$A$を$\...

上界･下界のイメージ･例･意義

具体的な$\mathbb{R}$の空でない部分集合を通して，上界･下界を確認しよう．

以下，$\mathbb{R}$の区間の上界･下界を考えることにする．区間についての詳細は次の記事を参照するとよい．

記事の公開までもう少しお待ち下さい！

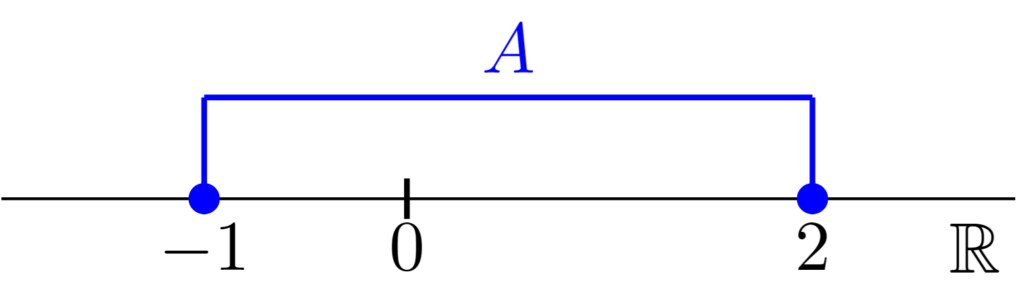
まず，$A=[-1,2]=\{ x\mid -1\le x\le 2\}$とおく．$A$の最大値は$2$であり，$A$の最小値は$-1$である．最大値･最小値はそれぞれ上界･下界の一種であるから，$A$は有界である．

また，例えば$3$も$A$の上界であり，$-2$も$A$の下界である．一般に，$A$の上界全体の集合を$U(A)$，下界全体の集合を$L(A)$とすると，$U(A)=\{ x\in \mathbb{R}\mid x\ge 2\}$であり，$L(A)=\{ x\in \mathbb{R}\mid x\le -1\}$である．

実際，任意の$a\ge 2,b\le -1,x\in A$に対し，$b\le -1\le x\le 2\le a$となり，$a$，$b$はそれぞれ$A$の上界，下界である．
また，$a<2$のとき，$2\in A$より$a$は$A$の上界でない．さらに，$b>-1$のとき，$-1\in A$より$b$は$A$の下界でない．

このように，上界･下界は複数存在することがある．一方で，最大値･最小値や上限･下限は，存在するとしても，1つしか存在しない(以下の記事を参照せよ)．

最大値･最小値～定義･イメージ･例を解説～

記事の公開までもう少しお待ち下さい！

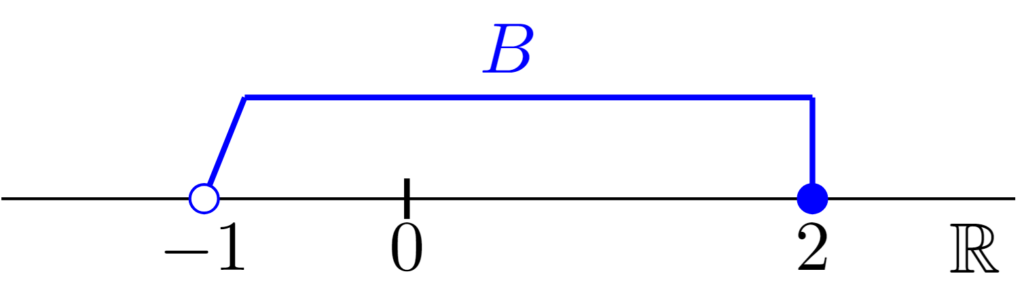
次に，$B=(-1,2]=\{ x\mid -1<x\le 2\}$とおく．$B$の最大値は$2$であり，最小値は存在しない．上と同様の議論により，$B$の上界全体の集合を$U(B)$とすると，$U(B)=\{ x\in \mathbb{R}\mid x\ge 2\}$である．特に，$B$の最大値$2$は$B$の上界でもある．一方で，$B$の下界全体の集合を$L(B)$とすると，$L(B)=\{ x\in \mathbb{R}\mid x\le -1\}$である．これも上と同様の議論により示すことができるのだが，重要なのは$-1$が$B$の下界であるという点である．$-1$は$B$の最小値ではないものの，$B$の下界である．

$b>-1$のとき，$b$が$B$の下界でないことを，自分の手で証明してみるとよい．

解答例

$b>-1$のとき，ある$x\in B$が存在し，$x<b$となることを示せばよい．
任意の$y\in B$に対し，$-1<y\le 2$
つまり，$-1<x<b$となる$x\in B$が存在するかどうかを調べればよい．
$b$と$-1$の平均$\dfrac{b-1}{2}$を$x$とすればよさそう･･･？
でも，$x\in B$となるかどうかは分からない！
$b\le 5$のときは$x\in B$となり，この方法で証明できそう．
$b>5$のときは？
$2\in B$だから，定義より$b$は$B$の下界ではない．場合分けで示せるかも．

上のような考え方で$x$を見つけるとよい．あとは先程と同様に証明するだけ．

$x=\min \left\{ \dfrac{b-1}{2},2\right\}$とおく．
このとき$-1\le x<2$より$x\in B$
また，$x<b$
よって，$b$は$B$の下界でない．
したがって，示された．

したがって，$B$は有界である．

$B$のような集合では，最小値は存在しないが，$-1$は$B$の｢最小値のようなもの｣であると言える．しかし，最小値はあくまでも｢取ることのできる値のうち，最も小さい値｣を表している．つまり，$B$の元は$-1$という値を取ることはないため，最小値と呼ぶことはできない．そこで，そのような｢最小値のようなもの｣を表す，$B$の下限という概念を導入することになる．その広い概念として，$B$の下界という概念を考えるのである．

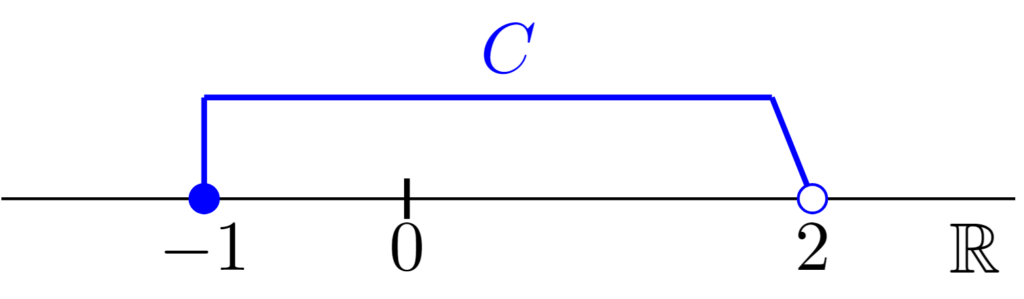
さらに，$C=[-1,2)=\{ x\mid -1\le x<2\}$とおく．$C$の最小値は$-1$であり，最大値は存在しない．

上と同様の議論により，$C$の上界全体の集合を$U(C)$とすると，$U(C)=\{ x\in \mathbb{R}\mid x\ge 2\}$である．また，$C$の下界全体の集合を$L(C)$とすると，$L(C)=\{ x\in \mathbb{R}\mid x\le -1\}$である．特に，$C$の最小値$2$は$C$の下界でもある．

したがって，$C$は有界である．

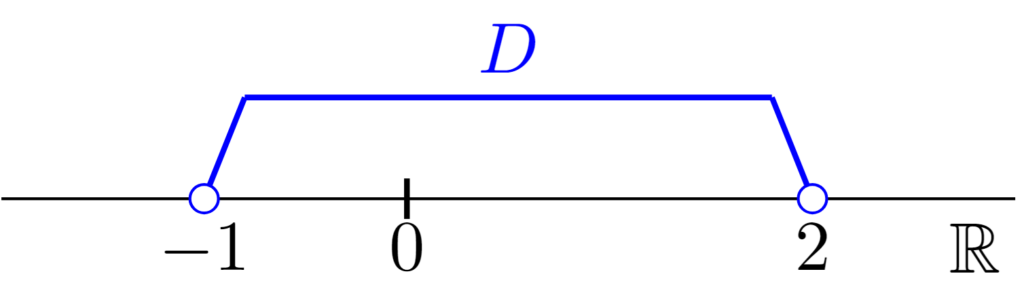
そして，$D=(-1,2)=\{ x\mid -1<x<2\}$とおくと，$D$には最大値も最小値も存在しない．

上と同様の議論により，$D$の上界全体の集合を$U(D)$とすると，$U(D)=\{ x\in \mathbb{R}\mid x\ge 2\}$である．また，$D$の下界全体の集合を$L(D)$とすると，$L(D)=\{ x\in \mathbb{R}\mid x\le -1\}$である．

したがって，$D$は有界である．

ここで，$A,B,C,D$の上界全体の集合と下界全体の集合がすべて等しいことに気づいただろうか．よく考えてみると，$A,B,C,D$はほとんど同じような区間を表している．端点を含んでいるかどうかが異なっているだけだ．つまり，上界と下界(上限と下限)によって，$A,B,C,D$の｢類似性｣が明らかになり，最大値と最小値によって，$A,B,C,D$の｢違い｣が明らかになると捉えることができる．

また，次のような集合の場合も，同様に上界･下界の存在性を確認することができる．

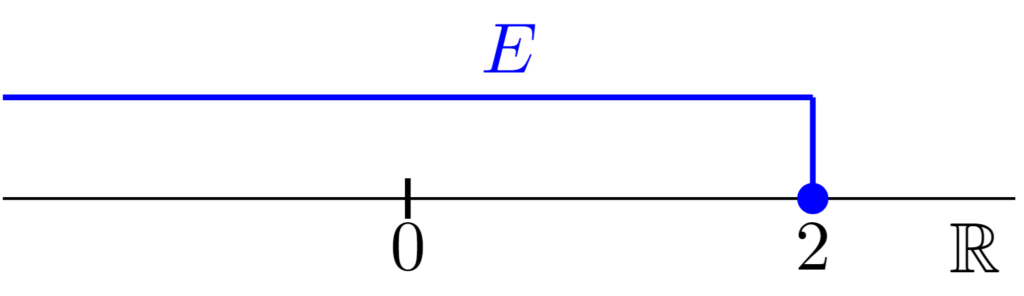
$E=(-\infty ,2]=\{ x\mid x\le 2\}$の最大値は$2$，最小値は存在しない．$E$の上界全体の集合を$U(E)$とすると，$U(E)=\{ x\in \mathbb{R}\mid x\ge 2\}$である．また，$E$の下界は存在しない．実際，任意の$t\in \mathbb{R}$に対し，$\min \{ 2,t-1\}\in E$が存在し，$\min \{ 2,t-1\} <t$となる．

したがって，$E$は上に有界であり，下に有界でない．

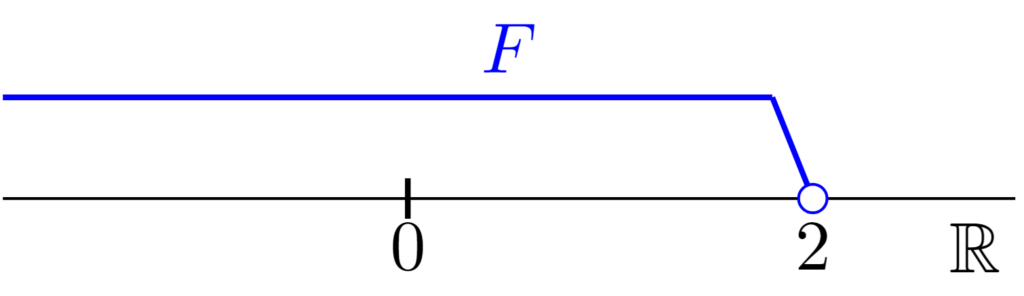
$F=(-\infty ,2)=\{ x\mid x<2\}$の最大値及び最小値は存在しない．$F$の上界全体の集合を$U(F)$とすると，$U(F)=\{ x\in \mathbb{R}\mid x\ge 2\}$である．また，$F$の下界は存在しない．実際，任意の$t\in \mathbb{R}$に対し，$\min \{ 1,t-1\}\in F$が存在し，$\min \{ 1,t-1\} <t$となる．

したがって，$F$は上に有界であり，下に有界でない．

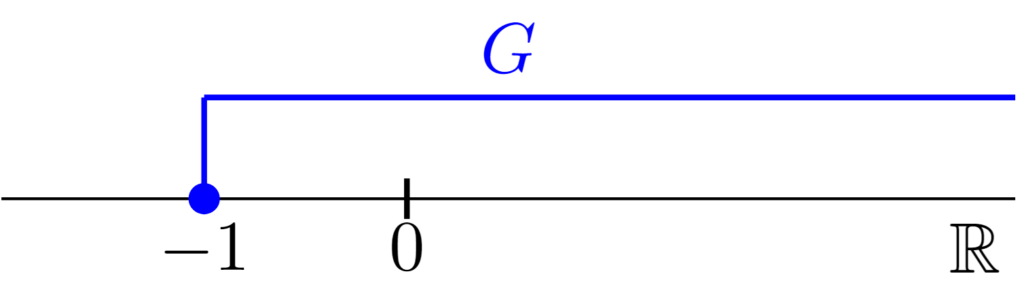
$G=[-1,\infty )=\{ x\mid x\ge -1\}$の最小値は$-1$，最大値は存在しない．$G$の下界全体の集合を$L(G)$とすると，$L(G)=\{ x\in \mathbb{R}\mid x\le -1\}$である．また，$G$の上界は存在しない．

したがって，$G$は下に有界であり，上に有界でない．

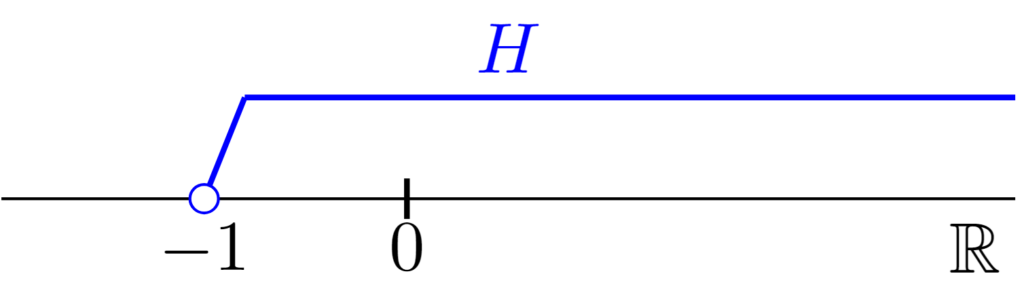
$H=(-1,\infty )=\{ x\mid x>-1\}$の最大値及び最小値は存在しない．$H$の下界全体の集合を$L(H)$とすると，$L(H)=\{ x\in \mathbb{R}\mid x\le -1\}$である．また，$H$の上界は存在しない．

したがって，$H$は下に有界であり，上に有界でない．

まとめると，空でない$\mathbb{R}$の部分集合$I$に対し，$I$の上界及び下界が存在するならば，それは上図のようになる．もちろん，$I$が一つの繋がった区間を表していたり，一つの繋がった区間が複数合わさった集合を表していたりすることに注意が必要である．

関連内容

上界･下界と最大値･最小値

ここまで，最大値･最小値は上界･下界の一種であると説明してきた．これは定義より明らかであるが，念の為証明しておこう．

命題1

$A$を$\mathbb{R}$の空でない部分集合とする．

$A$に最大値$\max A$が存在するとき，$\max A$は$A$の上界である．
$A$に最小値$\min A$が存在するとき，$\min A$は$A$の下界である．

証明

$A\subset \mathbb{R}$より，$\max A\in A$であるから，$\max A\in \mathbb{R}$
最大値の定義より，任意の$x\in A$に対し，$x\le \max A$となるから，定義より，$\max A$は$A$の上界である．$\blacksquare$
$A\subset \mathbb{R}$より，$\min A\in A$であるから，$\min A\in \mathbb{R}$
最小値の定義より，任意の$x\in A$に対し，$\min A\le x$となるから，定義より，$\min A$は$A$の下界である．$\blacksquare$

そして，区間の例と同様に考えることにより，次の命題を得る．

命題2

$A$を$\mathbb{R}$の空でない部分集合とし，$A$の上界全体の集合を$U(A)$，下界全体の集合を$L(A)$とする．

$A$に最大値$\max A$が存在するとき，$U(A)=\{ x\in \mathbb{R}\mid x\ge \max A\}$
$A$に最小値$\min A$が存在するとき，$L(A)=\{ x\in \mathbb{R}\mid \min A\le x\}$

証明

命題2より，任意の$a\in \{ x\in \mathbb{R}\mid x\ge \max A\} ,x\in A$に対し$x\le \max A\le a$
よって，$a$は$A$の上界である．
ここで，$b\not\in \{ x\in \mathbb{R}\mid x\ge \max A\}$のとき，$b<\max A$
$\max A\in A$であるから，$b$は$A$の上界でない．
したがって，$U(A)=\{ x\in \mathbb{R}\mid x\ge \max A\}$である．$\blacksquare$
命題2より，任意の$a\in \{ x\in \mathbb{R}\mid \min A\le x\} ,x\in A$に対し$a\le \min A\le x$
よって，$a$は$A$の下界である．
ここで，$b\not\in \{ x\in \mathbb{R}\mid \min A\le x\}$のとき，$b>\min A$
$\min A\in A$であるから，$b$は$A$の下界でない．
したがって，$L(A)=\{ x\in \mathbb{R}\mid \min A\le x\}$である．$\blacksquare$

上界･下界に似た概念

上界･下界に似た概念として，次のようなものがある．上界･下界との違いを認識する必要がある．

定義2

$A$を$\mathbb{R}$の空でない部分集合とする．ある$M\in \color{red}{A}$が存在し，任意の$x\in A$に対し，$x\le M$となるとき，$M$を$A$の最大値(maximum)という．また，ある$m\in \color{red}{A}$が存在し，任意の$x\in A$に対し，$m\le x$となるとき，$m$を$A$の最小値(minimum)という．

定義3

$A$を$\mathbb{R}$の空でない部分集合とし，$A$の上界全体の集合を$U(A)$，下界全体の集合を$L(A)$とする．$U(A)$に最小値$\alpha$が存在するとき，$\alpha$を$A$の上限(supremum)(または最小上界(least upper bound))といい，$\sup A$(または$\operatorname{lub}A$)で表す．また，$L(A)$に最小値$\beta$が存在するとき，$\beta$を$A$の下限(infimum)(または最大下界(greatest lower bound))といい，$\inf A$(または$\operatorname{glb}A$)で表す．

それぞれ記事を公開しているため，合わせて参照するとよい．